Functii cu proprietatea lui Darboux
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietaea lui Darboux: definitie, teorema de caracterizare; teorema valorilor intermediare, exemplu.
Domenii: Functii continue
Următorul rezultat ne ajută la a demonstra că o funcţie are proprietatea lui Darboux pe un interval.
Teorema 1: O funcţie 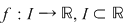 interval are proprietatea lui Darboux pe intervalul interval are proprietatea lui Darboux pe intervalul 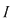 dacă şi numai dacă imaginea oricărui interval prin dacă şi numai dacă imaginea oricărui interval prin 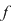 este tot un interval. este tot un interval.
Sintetizând teorema , 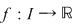 are proprietatea lui Darboux are proprietatea lui Darboux 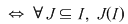 interval. interval.
Exemplu Fie 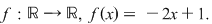 Vom determina că Vom determina că 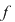 are proprietatea lui Darboux pe are proprietatea lui Darboux pe 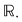
Fie 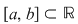 un interval. un interval.

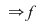 transformă intervale în intervale transformă intervale în intervale
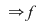 are proprietatea lui Darboux. are proprietatea lui Darboux.
Următoarea lemă este un rezultat necesar la demonstrarea unei teoreme ce va fi enunţată ulterior, dar este şi un rezultat folositor în rezolvarea unor probleme:
Lemă. Dacă 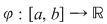 este o funcţie continuă şi este o funcţie continuă şi 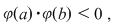 atunci există cel puţin un punct atunci există cel puţin un punct 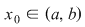 astfel încât astfel încât 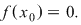
Altfel exprimat acest rezultat :
- dacă o funcţie 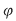 continuă pe un interval, admite două valori de semn opus, atunci funcţia respectivă are o rădăcină în intervalul respectiv. continuă pe un interval, admite două valori de semn opus, atunci funcţia respectivă are o rădăcină în intervalul respectiv.
Exemplu. Fie funcţia 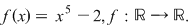 Se observă că Se observă că 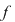 este continuă şi este continuă şi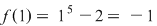
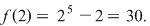
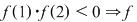 are o rădăcină în intervalul are o rădăcină în intervalul 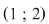
Materiale Didactice Asemanatoare
 Inversarea functiilor continue Inversarea functiilor continue
|