| |
 Filtre |
Biblioteca
In cadrul bibliotecii online poti studia 12 articole, 179 lectii.
Articolul zilei: Inmultirea numerelor complexe
Înmulţirea numerelor complexe
Fie 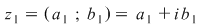
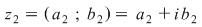
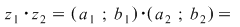
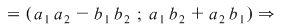
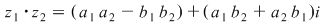
Se observă că făcând produsul
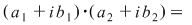
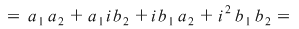
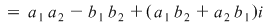
se obţine acelaşi rezultat ca aplicând definiţia produsului 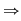 pentru a efectua produsul a două numere complexe în formă algebrică se înmulţeşte fiecare termen al primei paranteze cu fiecare termen din a doua paranteză şi se adună rezultatele. Se ţine cont de faptul că pentru a efectua produsul a două numere complexe în formă algebrică se înmulţeşte fiecare termen al primei paranteze cu fiecare termen din a doua paranteză şi se adună rezultatele. Se ţine cont de faptul că 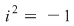 . .
Definitii echivalente pentru continuitatea unei functii intr-un punct
Continuitatea unei functii intr-un punct: scurt istoric, exemle de functii ale caror grafice sunt “intrerupte” sau au “salturi”, definitie punct de acumulare, definitie continuitate intr-un punct, teorema de caracterizare cu siruri, definitie punct de discontinuitate, definitie punct de discontinuitate de prima speta, definitie punct de discontinuitate de a doua speta, 4 exemple.
Vezi intregul articol | Radacinile de ordin n ale unitatii
Radacinile de ordin n ale unitatii. Interpretare geometrica.
Vezi intregul articol | Punct de acumulare
Puncte de acumulare, puncte isolate: definitii, exemple.
Vezi intregul articol | Functii reale de variabila reala - partea III
Functia rationala, exemple. Functia putere, exemple. Functia radical, exemple. Functia exponentiala: monotonie, marginire, bijectivitate. Functia logaritmica: monotonie, marginire, bijectivitate. Aplicatii: exercitii de tipul: determinarea domeniului maxim de definitie al unor compuse de functii descries mai sus.
Vezi intregul articol |
Materiale didactice
|
| |
| |