Aplicatii ale proprietatii lui Darboux
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Existenta zerourilor unei functii continue al carei semn variaza pe un interval; exemplu. Semnul unei functii continue, proprietatea de inertie a functiilor continue, exemple.
Domenii: Functii continue
 APLICAŢII ALE PROPRIETĂŢII LUI DARBOUX
APLICAŢII ALE PROPRIETĂŢII LUI DARBOUX
I. REZOLVAREA UNOR ECUAŢII
O metodă pentru rezolvarea unor ecuaţii este folosirea lemei ajutătoare, în demonstrarea teoremei valorilor intermediare:
Lemă. Fie o funcţie 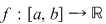 o funcţie continuă pentru care o funcţie continuă pentru care 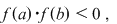
atunci 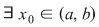 pentru care pentru care 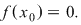 (Ecuaţia (Ecuaţia 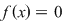 are cel puţin o soluţie în intervalul are cel puţin o soluţie în intervalul 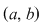 ) )
Dacă, în plus, funcţia 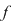 este strict crescătoare (sau strict descrescătoare) pe este strict crescătoare (sau strict descrescătoare) pe 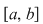 atunci atunci 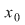 este soluţie unică. este soluţie unică.
Exemplu
Fie ecuaţia 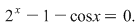
Deoarece 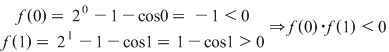
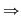 ecuaţia ecuaţia 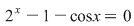 are cel puţin o soluţie în intervalul are cel puţin o soluţie în intervalul 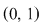
II. SEMNUL UNEI FUNCŢII
Dacă o funcţie 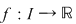 este o funcţie continuă pe este o funcţie continuă pe 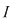 şi dacă şi dacă 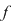 nu se anulează în niciunul dintre punctele intervalului nu se anulează în niciunul dintre punctele intervalului 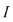 (ecuaţia (ecuaţia 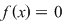 nu are soluţii pe nu are soluţii pe 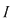 ), atunci funcţia are semn constant pe ), atunci funcţia are semn constant pe 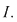
Într-adevăr, dacă presupunem prin absurd că 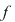 nu are semn constant pe nu are semn constant pe 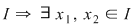 pentru care pentru care 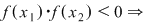 din lemă că din lemă că 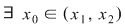 astfel încât astfel încât 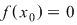 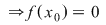 are soluţii pe are soluţii pe 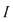 - imposibil (se contrazice faptul că ecuaţia - imposibil (se contrazice faptul că ecuaţia 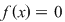 nu are soluţii pe nu are soluţii pe 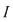 ). ).
În general, a studia semnul unei funcţii înseamnă a indica mulţimile de puncte în care funcţia este pozitivă sau negativă. Vom da o regulă practică importantă în stabilirea semnului unor funcţii elementare.
Să presupunem că toate zerourile reale ale unei funcţii continue 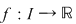 sunt sunt
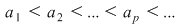
|