| |
 Optiuni  Inapoi la biblioteca |
Functii reale de variabila reala - partea I
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 28 Mai 2008, nivel de dificultate  . .
Functii pare, functii impare, exemple.Functii periodice, exemple.Functia lui Dirichlet. Functii monotone. Functii marginite, exemple.
Domenii: ---
Exemplu:
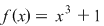
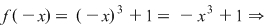
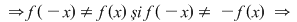
 nu este nici pară nici impară nu este nici pară nici impară
- FUNCŢIE PERIODICĂ
O funcţie 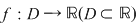 se numeşte periodică de perioadă se numeşte periodică de perioadă 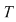 dacă pentru dacă pentru 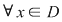 avem avem 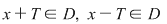 şi şi 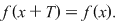
În acest caz, pentru orice 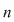 întreg nenul, întreg nenul, 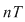 este perioadă pentru este perioadă pentru 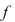 , iar mulţimea , iar mulţimea 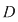 este mărginită. este mărginită.
Dacă există o cea mai mică perioadă strict pozitivă, aceasta se numeşte perioadă principală a lui 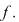
Se poate face studiul lui 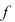 pe un interval de lungime cât perioada principală, extinzându-se proprietăţile la tot domeniul. pe un interval de lungime cât perioada principală, extinzându-se proprietăţile la tot domeniul.
Exemple:
1) Funcţiile 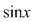 şi şi 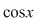 sunt periodice de perioadă sunt periodice de perioadă 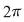 . .
|
| |
| |