| |
 Optiuni  Inapoi la biblioteca |
Functii reale de variabila reala - partea I
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 28 Mai 2008, nivel de dificultate  . .
Functii pare, functii impare, exemple.Functii periodice, exemple.Functia lui Dirichlet. Functii monotone. Functii marginite, exemple.
Domenii: ---
FUNCŢII MĂRGINITE
Definiţie:
O funcţie 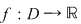 se numeşte se numeşte
a) mărginită superior dacă mulţimea valorilor ei 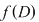 este majorată, adică este majorată, adică 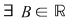 astfel încât astfel încât 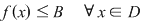
b) mărginită inferior, dacă mulţimea valorilor ei 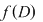 este minorată, adică este minorată, adică 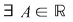 astfel încât astfel încât 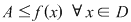
c) mărginită dacă este mărginită şi inferior şi superior adică 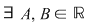 astfel încât astfel încât 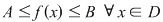 sau, altfel, sau, altfel, 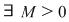 astfel încât astfel încât 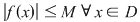
Exemple:
1) Funcţiile 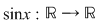 şi şi 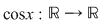 sunt mărginite deoarece sunt mărginite deoarece 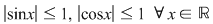
2) Funcţia 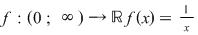 este nemărginită deoarece, pentru este nemărginită deoarece, pentru 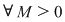
luând 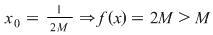
Restricţionând 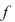 la orice interval de forma la orice interval de forma 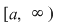 cu cu 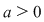 , se observă că , se observă că 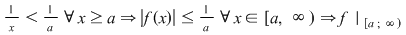 este mărginită. este mărginită.
|
| |
| |