Inversarea functiilor continue
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Teorema de caracterizare a functiilor cu proprietatea lui Darboux. Teorema valorilor intermediare. Exemple. Teorema: orice functie continua si injectiva pe un interval este strict monotona; orice functie continua pe un interval si surjectiva este bijectiva daca si numai daca este strict monotona; exemple.
Domenii: Functii continue
Teorema 3: Orice funcţie continuă şi injectivă pe un interval 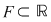 este strict monotonă. este strict monotonă.
 Folosind rezultatele enunţate anterior suntem în măsură să ne ocupăm de problema inversării funcţiilor continue. Folosind rezultatele enunţate anterior suntem în măsură să ne ocupăm de problema inversării funcţiilor continue.
Teorema 4: Fie 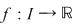 o funcţie continuă pe o funcţie continuă pe 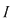 şi şi 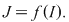
Funcţia 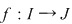 este bijectivă este bijectivă  este strict monotonă şi în acest caz funcţia este strict monotonă şi în acest caz funcţia 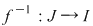 este continuă şi strict monotonă. este continuă şi strict monotonă.
 Acest rezultat ne asigură că funcţiile trigonometrice inverse (arcsin, arccos, arctg şi arcctg), funcţia radical şi funcţia logaritmică sunt funcţii continue şi strict monotone. Acest rezultat ne asigură că funcţiile trigonometrice inverse (arcsin, arccos, arctg şi arcctg), funcţia radical şi funcţia logaritmică sunt funcţii continue şi strict monotone.
 Un alt rezultat extrem de folositor şi în capitolul următor este demonstrarea bijectivităţii unei funcţii Un alt rezultat extrem de folositor şi în capitolul următor este demonstrarea bijectivităţii unei funcţii 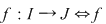 este continuă pe este continuă pe 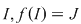 şi şi 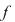 strict monotonă. strict monotonă.
Exemplu: Fie funcţia 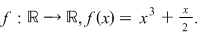 Să se demonstreze că funcţia este bijectivă. Să se demonstreze că funcţia este bijectivă.
Soluţie : 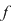 este funcţie continuă fiind funcţie elementară (polinomială). este funcţie continuă fiind funcţie elementară (polinomială).
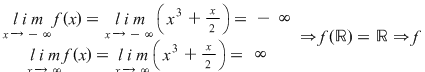 este surjectivă. este surjectivă.
Se demonstrează monotonia :
Fie 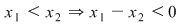
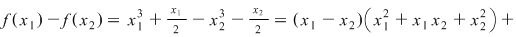
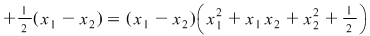
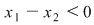
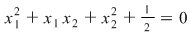 . (Se consideră ca fiind ecuaţie în . (Se consideră ca fiind ecuaţie în 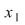 ) )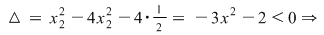 nu are soluţii reale nu are soluţii reale 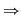 este pozitivă este pozitivă
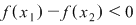 pentru pentru 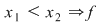 strict crescătoare strict crescătoare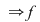 injectivă. injectivă.
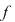 surjectivă şi injectivă surjectivă şi injectivă 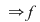 bijectivă. bijectivă.
Materiale Didactice Asemanatoare
 Functii cu proprietatea lui Darboux Functii cu proprietatea lui Darboux
|