 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Asupra unor probleme de teoria grupurilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
În aceasta nota vom prezenta unele rezultate din teoria grupurilor, insistând asupra teoremei lui Lagrange si asupra notiunii de ordin al unui element într-un grup finit, iar apoi vom rezolva 7 probleme de grupuri finite abeliene aplicand aceste doua rezultate. Remarcam faptul ca vom prezenta teorema lui Lagrange evitând notiunile de relatie de echivalenta si multime factor, care sunt incomode pentru o mare parte din elevi.
Domenii: Grupuri
b) Din teorema lui Lagrange rezultă că 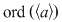 divide divide 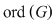 şi cum şi cum 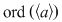 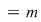 , rezultă , rezultă 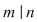 . .
c) 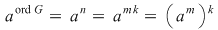 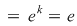 . .
d) Scriem 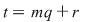 cu cu 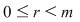 şi atunci: şi atunci: 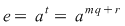 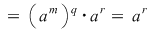 , adică , adică 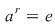 . Dacă . Dacă 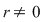 , cum , cum 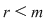 , obţinem o contradicţie, , obţinem o contradicţie, 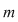 fiind cel mai mic număr natural pentru care fiind cel mai mic număr natural pentru care 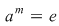 . Prin urmare, . Prin urmare, 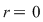 , adică , adică 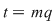 , deci , deci 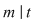 . .
e) Fie 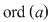 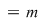 şi şi 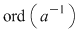 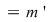 , adică , adică 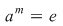 şi şi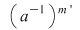 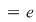 , de unde , de unde 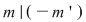 , deci , deci 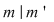 . Analog, se arată că . Analog, se arată că 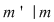 şi în concluzie şi în concluzie 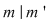 . .
2.5. Fie 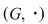 un grup comutativ finit cu elementul neutru un grup comutativ finit cu elementul neutru 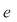 şi şi 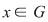 . Dacă . Dacă 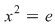 pentru mai mult de jumătate din elementele grupului, să se arate că grupul este abelian. pentru mai mult de jumătate din elementele grupului, să se arate că grupul este abelian.
Soluţie: Mulţimea 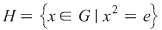 este un subgrup al lui este un subgrup al lui 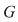 . Într-adevăr, dacă . Într-adevăr, dacă 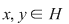 avem avem 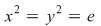 şi cum şi cum 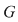 este grup abelian, putem scrie: este grup abelian, putem scrie:
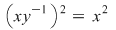
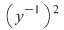  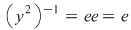 , adică , adică 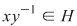 . Dacă . Dacă 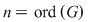 şi şi 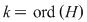 , atunci, conform teoremei lui Lagrange, obţinem , atunci, conform teoremei lui Lagrange, obţinem 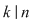 , adică , adică 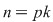 şi cum, din ipoteză, şi cum, din ipoteză, 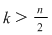 , adică , adică 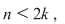 obţinem obţinem 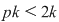 sau sau 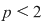 , şi cum , şi cum 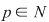 , rezultă , rezultă 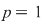 . Prin urmare, . Prin urmare, 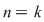 , adică , adică 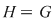 , şi de aici , şi de aici 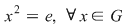 , deci grupul , deci grupul 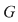 este abelian. este abelian.
Observaţie: Nu putem avea 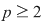 , pentru că ar rezulta , pentru că ar rezulta 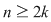 , ceea ce contrazice faptul că , ceea ce contrazice faptul că 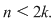
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
Bibliografie
| 1. Probleme de structuri algebrice - Nastasescu C., Tena M., Otarasanu I., Andrei Gh. - Editura: Academiei Romane - Bucuresti (anul 1988) | | 2. Semigrupuri, aplicatii - Nastasescu C., Otarasanu I. - Editura: Militara - Bucuresti (anul 1995) |
|