| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Asupra unor probleme de teoria grupurilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
În aceasta nota vom prezenta unele rezultate din teoria grupurilor, insistând asupra teoremei lui Lagrange si asupra notiunii de ordin al unui element într-un grup finit, iar apoi vom rezolva 7 probleme de grupuri finite abeliene aplicand aceste doua rezultate. Remarcam faptul ca vom prezenta teorema lui Lagrange evitând notiunile de relatie de echivalenta si multime factor, care sunt incomode pentru o mare parte din elevi.
Domenii: Grupuri
2.6. Să se arate că dacă într-un grup finit, mai mult de jumătate din elementele grupului comută cu toate elementele din grup, atunci grupul este abelian.
Soluţie: Dacă 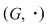 este grupul cu proprietatea din enunţul problemei şi este grupul cu proprietatea din enunţul problemei şi 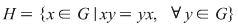 , atunci , atunci 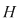 este subgrup al lui este subgrup al lui 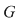 (numit centrul grupului (numit centrul grupului 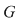 ). Conform ipotezei, ). Conform ipotezei, 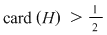 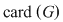 , iar din teorema lui Lagrange rezultă că există , iar din teorema lui Lagrange rezultă că există 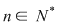 astfel încât: astfel încât: 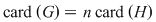 . Prin urmare . Prin urmare 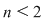 şi cum şi cum 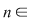 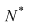 , rezultă , rezultă 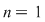 , adică , adică 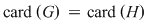 , de unde , de unde 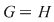 , adică , adică 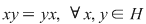 , ceea ce arată că grupul , ceea ce arată că grupul 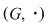 este abelian. este abelian.
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
Bibliografie
| 1. Probleme de structuri algebrice - Nastasescu C., Tena M., Otarasanu I., Andrei Gh. - Editura: Academiei Romane - Bucuresti (anul 1988) | | 2. Semigrupuri, aplicatii - Nastasescu C., Otarasanu I. - Editura: Militara - Bucuresti (anul 1995) |
|
| |
| |