 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Aplicatii ale integralei definite
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Calculul ariilor multimilor cuprinse intre doua curbe: definirea ariei unei multimi din plan ca limita unui sir de arii de reuniuni finite de dreptunghiuri, aria subgraficului unei functii continue si pozitive este egala cu integrala Riemann a acelei functii, demonstratie; aria multimii determinate de graficele a doua functii continue egala cu integrala Riemann a modulului diferentei celor doua functii, exemple. Volumul corpurilor de rotatie: definirea volumului unui corp de rotatie ca limita unui sir de volume de reuniuni finite de cilindrii plini; volumul unui corp de rotatie determinat de o functie continua este egal cu integrala Riemann a patratului acelei functii inmultita cu constanta pi, demonstratie; volumul unui corp de rotatie marginit de suprafetele obtinute prin rotatia graficelor a doua functii continue este egal cu integrala Riemann a diferentei patratelor celor doua functii inmultita cu constanta pi, exemple. Lungimea graficului unei functii derivabile cu derivate continua: definirea lungimii graficului unei functii derivabile cu derivate continua ca limita a lungimilor liniilor poligonale ce au varfurile pe grafic si teorema de calcul al acestei lungimi cu demonstratie; exemple. Aria suprafetelor de rotatie: definirea ariei suprafetei de rotatie a graficului unei functii continue si pozitive ca limita unui sir de arii ale suprafetelor de rotatie a liniilor poligonale corespunzatoare si teorema de calcul a acestei arii cu demonstratie, exemple.
Domenii: Aplicatii ale integrabilei Riemann
Rezultă că există 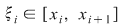 astfel încât astfel încât 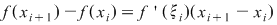 . Aplicând din nou lui . Aplicând din nou lui 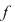 această teoremă pe fiecare interval această teoremă pe fiecare interval 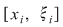 , , 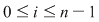 , obţinem că există , obţinem că există 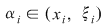 astfel încât astfel încât 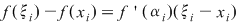 . Prin urmare, . Prin urmare,
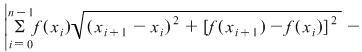
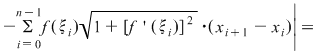
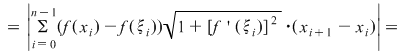
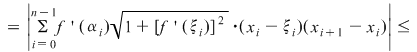
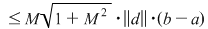 , unde am notat , unde am notat 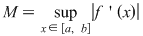 . Pe de altă parte, funcţia . Pe de altă parte, funcţia 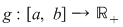 , , 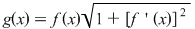 este funcţie continuă şi deci integrabilă. este funcţie continuă şi deci integrabilă.
Rezultă astfel că 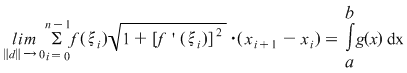 şi din inegalitatea precedentă deducem că şi din inegalitatea precedentă deducem că
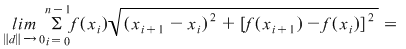
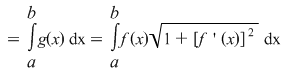 . .
Observaţii:
1. Dacă funcţia 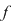 nu este pozitivă, atunci nu este pozitivă, atunci 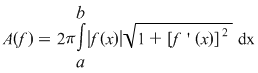 . Într-adevăr, în acest caz razele bazelor trunghiurilor de con considerate în demonstraţie sunt . Într-adevăr, în acest caz razele bazelor trunghiurilor de con considerate în demonstraţie sunt 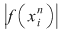 şi şi 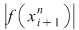 . Dacă definim . Dacă definim 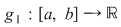 , , 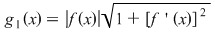 , atunci , atunci 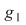 este funcţie continuă. este funcţie continuă.
2. Fie 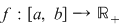 o funcţie continuă, derivabilă pe o funcţie continuă, derivabilă pe 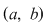 , cu derivata continuă pe , cu derivata continuă pe 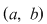 astfel încât funcţia astfel încât funcţia 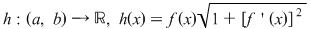 are limitele finite în punctele are limitele finite în punctele 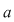 şi şi 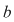 . Dacă . Dacă 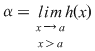 şi şi 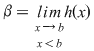 , atunci , atunci 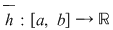 , ,  este continuă întrucât este prelungirea prin continuitate a lui este continuă întrucât este prelungirea prin continuitate a lui 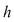 . Repetând raţionamentele din demonstraţia teoremei 4 pentru funcţia . Repetând raţionamentele din demonstraţia teoremei 4 pentru funcţia 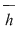 , rezultă că şi în acest caz , rezultă că şi în acest caz 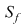 are arie şi aria sa are arie şi aria sa 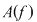 se poate calcula după formula se poate calcula după formula 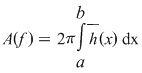 . .
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Elemente de analiza matematica vol. I - Ganga M. - Editura: MathPress |
|