 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Aplicatii ale integralei definite
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Calculul ariilor multimilor cuprinse intre doua curbe: definirea ariei unei multimi din plan ca limita unui sir de arii de reuniuni finite de dreptunghiuri, aria subgraficului unei functii continue si pozitive este egala cu integrala Riemann a acelei functii, demonstratie; aria multimii determinate de graficele a doua functii continue egala cu integrala Riemann a modulului diferentei celor doua functii, exemple. Volumul corpurilor de rotatie: definirea volumului unui corp de rotatie ca limita unui sir de volume de reuniuni finite de cilindrii plini; volumul unui corp de rotatie determinat de o functie continua este egal cu integrala Riemann a patratului acelei functii inmultita cu constanta pi, demonstratie; volumul unui corp de rotatie marginit de suprafetele obtinute prin rotatia graficelor a doua functii continue este egal cu integrala Riemann a diferentei patratelor celor doua functii inmultita cu constanta pi, exemple. Lungimea graficului unei functii derivabile cu derivate continua: definirea lungimii graficului unei functii derivabile cu derivate continua ca limita a lungimilor liniilor poligonale ce au varfurile pe grafic si teorema de calcul al acestei lungimi cu demonstratie; exemple. Aria suprafetelor de rotatie: definirea ariei suprafetei de rotatie a graficului unei functii continue si pozitive ca limita unui sir de arii ale suprafetelor de rotatie a liniilor poligonale corespunzatoare si teorema de calcul a acestei arii cu demonstratie, exemple.
Domenii: Aplicatii ale integrabilei Riemann
Pe de altă parte, să considerăm dreptunghiul 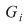 ce are baza intervalul ce are baza intervalul 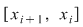 şi înălţimea şi înălţimea 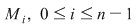 . Acest dreptunghi conţine porţiunea din mulţimea . Acest dreptunghi conţine porţiunea din mulţimea 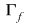 ce are proiecţia pe axa Ox intervalul ce are proiecţia pe axa Ox intervalul 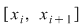 , iar aria sa este , iar aria sa este 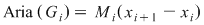 . Prin urmare, dacă notăm . Prin urmare, dacă notăm 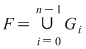 , atunci , atunci 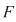 este o mulţime din este o mulţime din 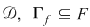 şi şi 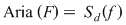 . .
Fie acum 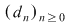 un şir de diviziuni ale intervalului un şir de diviziuni ale intervalului 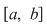 astfel încât astfel încât 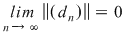 . Pentru fiecare . Pentru fiecare 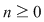 notăm cu notăm cu 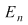 şi şi 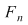 mulţimile din mulţimile din 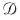 construite ca mai sus. Pentru orice construite ca mai sus. Pentru orice  avem că avem că 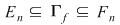 şi şi 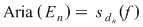 , , 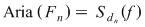 . Cum funcţia . Cum funcţia 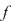 este continuă, deci integrabilă, rezultă că este continuă, deci integrabilă, rezultă că 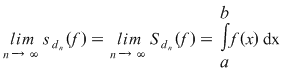 şi deci şi deci 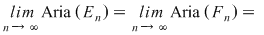
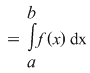 . Am obţinut astfel că mulţimea . Am obţinut astfel că mulţimea  are arie şi are arie şi 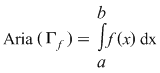 . .
Observaţie: Teorema 1. rămâne adevărată şi pentru funcţii 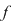 integrabile. În acest caz, reciproca sa este, de asemenea, adevărată: dacă integrabile. În acest caz, reciproca sa este, de asemenea, adevărată: dacă 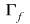 are arie, atunci are arie, atunci 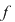 este integrabilă în sens Riemann. este integrabilă în sens Riemann.
Să considerăm acum două funcţii continue 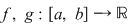 astfel încât astfel încât 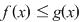 pentru orice pentru orice 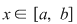 , deci graficul funcţiei , deci graficul funcţiei 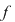 este situat sub graficul funcţiei este situat sub graficul funcţiei 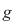 . .
Vom nota cu 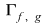 mulţimea mărginită de graficele celor două funcţii mulţimea mărginită de graficele celor două funcţii 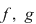 şi dreptele şi dreptele 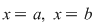 . Prin urmare, . Prin urmare,
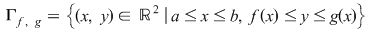 . .
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Elemente de analiza matematica vol. I - Ganga M. - Editura: MathPress |
|