Corpuri
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Mai 2009, nivel de dificultate  . .
Definitia corpurilor. Corpul claselor de resturi modulo p. Legatura dintre corpuri si inele integre.
Domenii: ---
Corpuri
1) Definiţie
Se numeşte corp un triplet 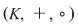 în care în care 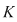 este o mulţime cu cel puţin două elemente, iar este o mulţime cu cel puţin două elemente, iar 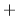 şi şi 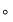 două operaţii pe două operaţii pe 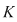 (numite "adunare" respectiv "înmulţire") satisfăcând trei axiome: (numite "adunare" respectiv "înmulţire") satisfăcând trei axiome:
a) 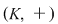 este un grup abelian cu elementul neutru notat este un grup abelian cu elementul neutru notat 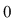 . .
b) 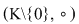 este un grup cu elemetul neutru notat este un grup cu elemetul neutru notat 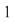 . .
c) Înmulţirea este distributivă faţă de adunare.
Grupul 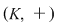 se numeşte grupul aditiv al corpului, iar grupul se numeşte grupul aditiv al corpului, iar grupul 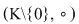 se numeşte grupul multiplicativ al elementelor nenule ale corpului. se numeşte grupul multiplicativ al elementelor nenule ale corpului.
Dacă, în plus, este satisfăcută şi axioma a patra:
d) Înmulţirea este comutativă (echivalent spus, în axioma b) scriem "grup abelian"), atunci tripletul 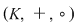 se numeşte corp comutativ. se numeşte corp comutativ.
Comparând cu definiţia inelului şi ţinând seama că într-un inel cu cel puţin două elemente avem 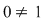 , putem da următoarea: , putem da următoarea:
2) Definiţie echivalentă
Se numeşte corp un inel 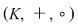 cu cu 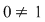 (echivalent spus, având cel puţin două elemente) în care orice element nenul este inversabil (echivalent spus, (echivalent spus, având cel puţin două elemente) în care orice element nenul este inversabil (echivalent spus, 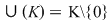 ) )
Exemple:
1. 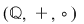 este un corp comutativ, numit corpul numerelor raţionale. este un corp comutativ, numit corpul numerelor raţionale.
2. 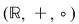 este un corp comutativ, numit corpul numerelor reale. este un corp comutativ, numit corpul numerelor reale.
3. 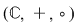 este un corp comutativ, numit corpul numerelor complexe. este un corp comutativ, numit corpul numerelor complexe.
4. Dacă 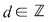 este un întreg care nu este pătrat perfect şi notăm este un întreg care nu este pătrat perfect şi notăm
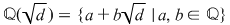
unde 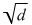 este o soluţie fixată (în este o soluţie fixată (în 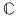 ) a ecuaţiei ) a ecuaţiei 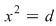 , atunci , atunci 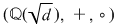 este un corp comutativ numit corp pătratic. Într-adevăr, este un corp comutativ numit corp pătratic. Într-adevăr, 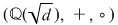 este un inel comutativ cu este un inel comutativ cu 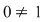 (verificarea axiomelor inelului comutativ poate constitui o temă simplă) şi în care orice element este inversabil, căci dacă (verificarea axiomelor inelului comutativ poate constitui o temă simplă) şi în care orice element este inversabil, căci dacă 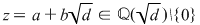 , atunci există numărul complex , atunci există numărul complex 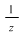 şi avem: şi avem:
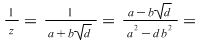
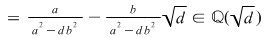
|