| |
 Optiuni  Inapoi la biblioteca |
Despre continuitatea functiilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XI-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Continuitatea functiilor: scurt istoric. Punct de acumulare: definitie, exemple.Punct izolat, definitie, exemple. Definitii ale limitei unei functii intr-un punct. Definitia continuitatii unei functii intr-un punct,exemple, tipuri de probleme.
Domenii: ---
4. Funcţia 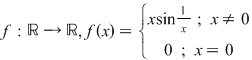 este continuă în 0. este continuă în 0.
Soluţie :
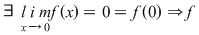 continuă în 0. continuă în 0.
5. Funcţia 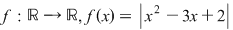 este continuă în 1 şi 2. este continuă în 1 şi 2.
Soluţia 1 :
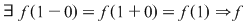 continuă în 1 continuă în 1
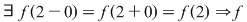 continuă în 2 continuă în 2
Soluţia 2 :
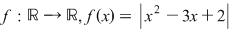 este compusa funcţiilor: este compusa funcţiilor:
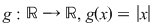
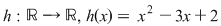
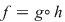
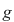 este continuă : este continuă : 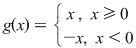 fiind polinomială pe fiind polinomială pe 
iar limitele laterale în 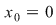 sunt egale şi egale cu sunt egale şi egale cu 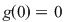 , deci , deci 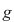 continuă şi în continuă şi în 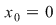 . .
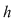 este continuă fiind polinom. este continuă fiind polinom.
Deci 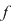 este continuă pe este continuă pe 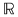 fiind compusă din funcţii continue pe fiind compusă din funcţii continue pe 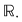
6. Să se determine toate funcţiile reale, continue, 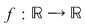 cu cu 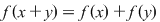
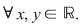
Soluţie :
Avem 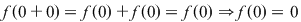
|
| |
| |