 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Doua probleme de grupuri
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Prima problema se refera la "slabirea" axiomelor grupului, iar cea de-a doua la compatibilitatea ecuatiei binome într-un grup finit.
Domenii: Grupuri
Considerăm acum elementul 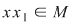 , care este şi el lateral simetrizabil, să zicem la stânga, adică: , care este şi el lateral simetrizabil, să zicem la stânga, adică: 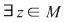 cu cu 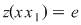 , adică , adică 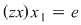 , deci , deci 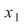 este simetrizabil la stânga şi atunci se continuă ca la implicaţia b) este simetrizabil la stânga şi atunci se continuă ca la implicaţia b) 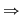 c), ajungându-se la concluzia că c), ajungându-se la concluzia că 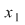 este şi simetric la dreapta al elementului este şi simetric la dreapta al elementului 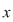 , deci , deci 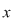 este simetrizabil. este simetrizabil.
Dacă 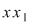 este simetrizabil la dreapta, este simetrizabil la dreapta, 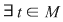 cu cu 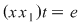 , adică , adică 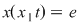 , deci , deci 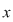 este şi simetrizabil la dreapta. Fiind simetrizabil la stânga şi la dreapta, este şi simetrizabil la dreapta. Fiind simetrizabil la stânga şi la dreapta, 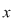 este simetrizabil, deoarece din este simetrizabil, deoarece din 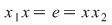 (am notat (am notat 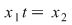 ) rezultă ) rezultă 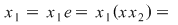
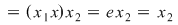 , adică simetricele la stânga şi la dreapta coincid. Aşadar, orice element , adică simetricele la stânga şi la dreapta coincid. Aşadar, orice element 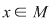 este simetrizabil, adică este simetrizabil, adică 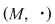 este grup. este grup.
COMENTARIU
Oricare din condiţiile b), c), d), e) reprezintă (de fapt) "slăbiri" ale sistemului axiomatic al grupului. Se poate merge chiar şi mai mult cu această "slăbire", presupunând, de exemplu, că 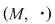 este doar un semigrup (vezi articolul referitor la structuri algebrice pregrupale) în care există element neutru la stânga (dreapta) şi fiecare element al acestui semigrup este simetrizabil la stânga (dreapta). este doar un semigrup (vezi articolul referitor la structuri algebrice pregrupale) în care există element neutru la stânga (dreapta) şi fiecare element al acestui semigrup este simetrizabil la stânga (dreapta).
Mai precis: dacă în semigrupul 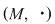 există există 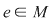 cu proprietatea cu proprietatea 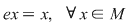 şi pentru orice şi pentru orice 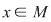 , există , există 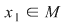 cu cu 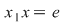 , atunci , atunci 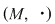 este un grup. este un grup.
Într-adevăr, mai întâi dovedim că pentru fiecare 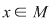 , simetricul său la stânga , simetricul său la stânga 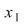 este şi simetric la dreapta (faţă de acelaşi element neutru la stânga este şi simetric la dreapta (faţă de acelaşi element neutru la stânga 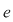 ). ).
Dacă 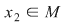 este simetricul la stânga al lui este simetricul la stânga al lui 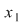 , adică , adică 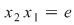 , avem: , avem:
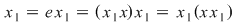 , de unde rezultă , de unde rezultă 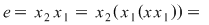
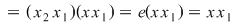 , adică , adică 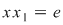 . Mai rămâne să arătăm că . Mai rămâne să arătăm că 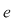 este element neutru la dreapta. Pentru orice este element neutru la dreapta. Pentru orice 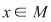 , notând cu , notând cu 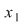 simetricul său (atât la stânga cât şi la dreapta) avem: simetricul său (atât la stânga cât şi la dreapta) avem: 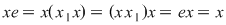 . .
Prin urmare, 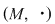 este grup şi comentariul se încheie. este grup şi comentariul se încheie.
P 2: Fie 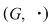 un grup multiplicativ cu un grup multiplicativ cu 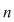 elemente. elemente.
Să se arate că:
I) Dacă 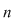 nu este divizibil cu nu este divizibil cu 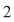 , atunci pentru orice , atunci pentru orice 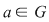 , ecuaţia , ecuaţia 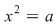 are o soluţie unică în grupul are o soluţie unică în grupul 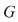 . .
II) Dacă 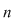 nu este divizibil cu nu este divizibil cu 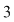 , atunci pentru orice , atunci pentru orice 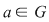 , ecuaţia , ecuaţia 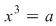 are o soluţie unică în grupul are o soluţie unică în grupul 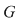 . .
Materiale Didactice Asemanatoare
 Asupra unor probleme de teoria grupurilor Asupra unor probleme de teoria grupurilor
 Structuri algebrice pregrupale Structuri algebrice pregrupale
 Un semigrup remarcabil Un semigrup remarcabil
Bibliografie
| 1. Probleme de structuri algebrice - Nastasescu C., Tena M., Otarasanu I., Andrei Gh. - Editura: Academiei Romane - Bucuresti (anul 1988) |
|