Un semigrup remarcabil
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 07 Feb 2008, nivel de dificultate  . .
Semigrupul relatiilor binare ale unei multimi: definitie, asociativitatea compunerii, existenta elementului neutru—diagonala acelei multimi.
Domenii: Lege de compozitie interna
 Un semigrup remarcabil
Un semigrup remarcabil
I. Introducere
1.1 Semigrupul este dubletul 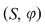 format din mulţimea nevidă format din mulţimea nevidă 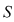 şi legea de compoziţie asociativă şi legea de compoziţie asociativă 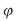 definită pe definită pe 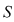 . .
Dacă, în plus, legea de compoziţie 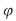 admite element neutru, semigrupul admite element neutru, semigrupul 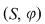 se numeşte monoid sau semigrup cu unitate. se numeşte monoid sau semigrup cu unitate.
Elementul 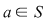 se numeşte element zero al semigrupului se numeşte element zero al semigrupului 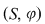 dacă dacă 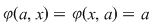 oricare ar fi oricare ar fi 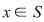 . .
Elementul 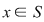 se numeşte element idempotent al semigrupului se numeşte element idempotent al semigrupului 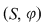 dacă dacă 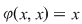
1.2 Se numeşte relaţie binară pe muţimea arbitrară 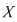 orice submulţime orice submulţime 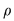 a produsului cartezian a produsului cartezian 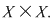
Dacă 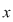 şi şi 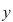 sunt două elemente arbitrare ale mulţimii sunt două elemente arbitrare ale mulţimii 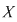 , iar , iar 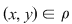 , vom spune că , vom spune că 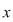 este în relaţia este în relaţia 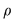 cu cu 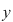 şi vom nota acest lucru prin şi vom nota acest lucru prin 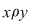 . Dacă . Dacă 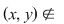 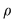 , atunci vom scrie , atunci vom scrie 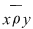 . .
Mai precizăm faptul că, dacă 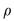 este o relaţie binară pe este o relaţie binară pe 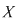 , atunci ea se numeşte: , atunci ea se numeşte:
a) reflexivă, dacă 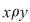 , oricare ar fi , oricare ar fi 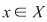 ; ;
b) simetrică, dacă oricare ar fi 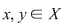 cu cu 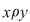 rezultă rezultă 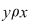 ; ;
c) tranzitivă, dacă oricare ar fi 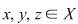 cu cu 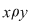 şi şi 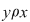 rezultă rezultă 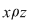 . .
În fine, dacă o relaţie binară este reflexivă, simetrică şi tranzitivă, atunci ea este o relaţie de echivalenţă.
Vom studia în continuare un semigrup remarcabil şi anume:
II. Semigrupul relaţiilor binare ale unei mulţimi
Dacă 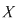 este o mulţime arbitrară şi notăm cu este o mulţime arbitrară şi notăm cu 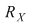 mulţimea tuturor relaţiilor binare definite pe mulţimea tuturor relaţiilor binare definite pe 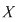 , atunci , atunci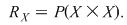 Pentru Pentru 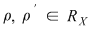 definim relaţia binară: definim relaţia binară: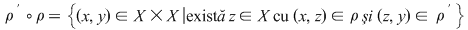
Relaţia binară 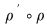 se numeşte compunerea relaţiei binare se numeşte compunerea relaţiei binare 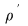 cu relaţia binară cu relaţia binară 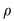 . De asemenea, pentru mulţimea arbitrară . De asemenea, pentru mulţimea arbitrară 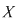 , vom nota: , vom nota:
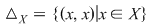 diagonala mulţimii diagonala mulţimii 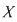 , care, evident, este o relaţie binară pe , care, evident, este o relaţie binară pe 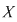 şi observăm că şi observăm că 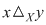 dacă şi numai dacă dacă şi numai dacă 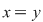 . Din acest motiv relaţia binară . Din acest motiv relaţia binară 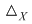 se numeşte egalitate pe mulţimea se numeşte egalitate pe mulţimea 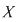 . .
Propoziţia 2.1
Operaţia de compunere a relaţiilor binare determină pe mulţimea 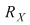 o structură de monoid având ca element neutru relaţia binară o structură de monoid având ca element neutru relaţia binară 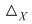 . În plus, muţimea vidă este elementul zero al acestui monoid. . În plus, muţimea vidă este elementul zero al acestui monoid.
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
Bibliografie
| 1. Elemente de teoria semigrupurilor - Nastasescu C., Otarasanu I. - Editura: Rotech-Pro - Bucuresti (anul 1999) |
|