 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Ecuatii algebrice de grad superior
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Teorema lui Bezout. Scurt istoric despre rezovarea ecuatiilor algebrice de grad 1-4. Teorema Abel-Ruffini si teorema d’Alembert-Gauss (teorema fundamentala a algebrei). Numere intregi negative, numere rationale, numere complexe ca radacini de ecuatii algebrice. Relatii intre radacini si coeficienti (relatiile lui Viete) cu exemple. Rezolvarea ecuatiilor binome. Exemple si figuri geometrice pentru gradele 3,4. Rezolvarea ecuatiilor bipatrate. Exemple.
Domenii: Polinoame
Exemplu:
Să se rezolve ecuaţia binomă: 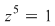
Avem 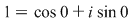 şi rădăcinile de ordin 5 ale unităţii sunt: şi rădăcinile de ordin 5 ale unităţii sunt: 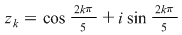 , , 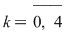 , adică: , adică: 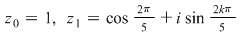 , , 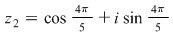 , , 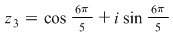 , , 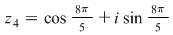 . .
Imaginile geometrice ale acestor numere sunt vârfurile pentagonului regulat înscris în cercul unitate.
(2) Ecuaţii bipătrate: Forma generală a ecuaţiilor bipătrate este: 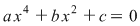 , , 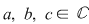 şi şi 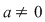 . În cazul general, rezolvarea ecuaţiei se face astfel: . În cazul general, rezolvarea ecuaţiei se face astfel:
- se face substituţia 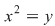 şi obţinem ecuaţia de gradul doi şi obţinem ecuaţia de gradul doi 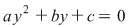
Această ecuaţie se numeşte rezolventa ecuaţiei anterioare, iar rădăcinile ei sunt:
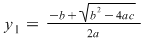 şi şi 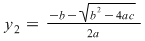
Din egalitatea 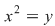 obţinem ecuaţiile obţinem ecuaţiile 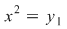 şi şi 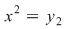 . Ecuaţia . Ecuaţia 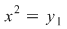 are rădăcinile: are rădăcinile:
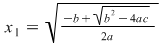 şi şi 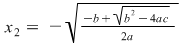
Ecuaţia 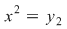 are rădăcinile: are rădăcinile:
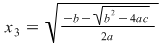 şi şi 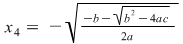
Numerele 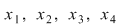 sunt rădăcinile ecuaţiei date. sunt rădăcinile ecuaţiei date.
Ele pot fi cuprinse în formula:
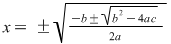 numită formula de rezolvare a ecuaţiei bipătrate. numită formula de rezolvare a ecuaţiei bipătrate.
Materiale Didactice Asemanatoare
 Aplicatii ale ecuatiilor algebrice de grad superior Aplicatii ale ecuatiilor algebrice de grad superior
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Soare N. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Elemente de Algebra - Ganga M. - Editura: MathPress |
|