| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Formula de integrare prin parti
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Formula de integrare prin parti: teorema cu demonstratie; orice functie continua cu exceptia unui numar finit de puncte, in care are discontinuitati de prima speta, este integrabila, demonstratie, exemplu; teorema (formula de schimbare de variabila) cu demonstratie, exemple.
Domenii: Functii integrabile Riemann
Formula de integrare prin părţi
Teorema (formula de integrare prin părţi)
Dacă 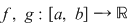 sunt funcţii derivabile şi cu derivatele continue, atunci: sunt funcţii derivabile şi cu derivatele continue, atunci:
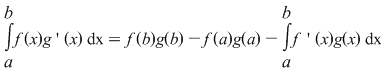 . .
Demonstraţie:
Funcţia 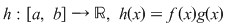 este derivabilă şi este derivabilă şi 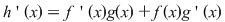 . .
Citim aceasta spunând că 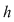 este o primitivă a funcţiei este o primitivă a funcţiei 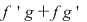 . Conform formulei Leibnitz-Newton, folosind şi proprietatea de liniaritate a integralei, obţinem . Conform formulei Leibnitz-Newton, folosind şi proprietatea de liniaritate a integralei, obţinem 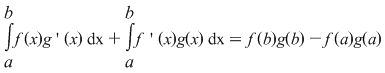 . .
Observaţie:
Formula din enunţ se scrie:
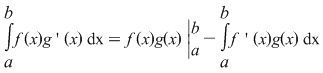
Propoziţia 2: Fie 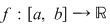 o funcţie continuă pe o funcţie continuă pe 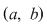 şi astfel încât în punctele şi astfel încât în punctele 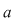 şi şi 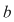 are limite finite. Atunci are limite finite. Atunci 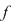 este integrabilă pe este integrabilă pe 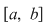 . .
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|
| |
| |