 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Formula de integrare prin parti
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Formula de integrare prin parti: teorema cu demonstratie; orice functie continua cu exceptia unui numar finit de puncte, in care are discontinuitati de prima speta, este integrabila, demonstratie, exemplu; teorema (formula de schimbare de variabila) cu demonstratie, exemple.
Domenii: Functii integrabile Riemann
Demonstraţie:
Să notăm 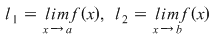 şi cu şi cu 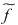 prelungirea prin continuitate a restricţiei funcţiei prelungirea prin continuitate a restricţiei funcţiei 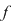 la la 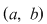 , adică: , adică:

Fie de asemenea 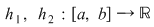 , ,
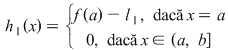
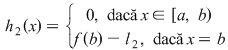
Funcţia 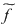 este integrabilă, deoarece este continuă, iar este integrabilă, deoarece este continuă, iar 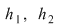 sunt strict integrabile, deoarece sunt monotone. sunt strict integrabile, deoarece sunt monotone.
Din 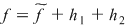 rezultă că funcţia rezultă că funcţia 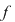 este integrabilă. Este util să reţinem că deoarece este integrabilă. Este util să reţinem că deoarece 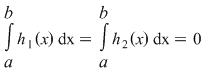 , rezultă , rezultă 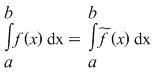 . .
Observaţii:
1) Afirmaţia din enunţ este nebanală dacă cel puţin unul dintre punctele 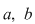 este punct de discontinuitate de prima speţă pentru funcţie. este punct de discontinuitate de prima speţă pentru funcţie.
2) O construcţie forţată a unei situaţii ca aceea din propoziţie este cea în care, pentru o funcţie continuă 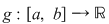 modificăm valorile în punctele modificăm valorile în punctele 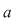 şi şi 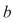 , adică considerăm , adică considerăm 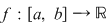 astfel încât astfel încât 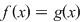 pentru orice pentru orice 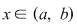 . Propoziţia spune că atunci . Propoziţia spune că atunci 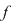 este integrabilă şi este integrabilă şi 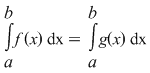 . .
O afirmaţie mai generală decât cea din propoziţia 2 este:
Teorema: Orice funcţie  , continuă cu excepţia unui număr finit de puncte unde are discontinuităţi de prima speţă, este integrabilă. , continuă cu excepţia unui număr finit de puncte unde are discontinuităţi de prima speţă, este integrabilă.
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|