 Optiuni  Da un Test Nou |
Formula de integrare prin parti
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Formula de integrare prin parti: teorema cu demonstratie; orice functie continua cu exceptia unui numar finit de puncte, in care are discontinuitati de prima speta, este integrabila, demonstratie, exemplu; teorema (formula de schimbare de variabila) cu demonstratie, exemple.
Domenii: Functii integrabile Riemann
Demonstraţie:
Ordonând punctele de discontinuitate, fie 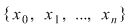 o diviziune a intervalului o diviziune a intervalului 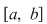 astfel încât funcţia admite limite laterale finite în fiecare punct astfel încât funcţia admite limite laterale finite în fiecare punct 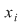 şi este continuă pe fiecare interval şi este continuă pe fiecare interval 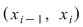 . Conform propoziţiei precedente, funcţia este integrabilă pe . Conform propoziţiei precedente, funcţia este integrabilă pe 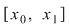 şi pe şi pe 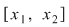 , iar apoi va rezulta că este integrabilă pe , iar apoi va rezulta că este integrabilă pe 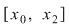 . După un număr finit de paşi vom obţine că funcţia este integrabilă pe . După un număr finit de paşi vom obţine că funcţia este integrabilă pe 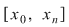 , adică pe , adică pe 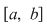 . .
Observaţie:
Din proprietatea de aditivitate a integralei şi propoziţia precedentă rezultă că 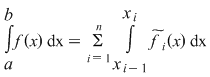 , unde , unde 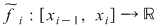 reprezintă prelungirea prin continuitate a restricţiei reprezintă prelungirea prin continuitate a restricţiei 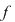 la intervalul la intervalul 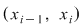 . .
Exemplu:
Să studiem integrabilitatea funcţiei 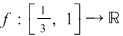 definită prin definită prin 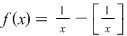 . .
Avem: 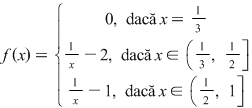
Se observă că 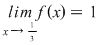 , , 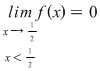 , , 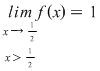 şi că funcţia este continuă cu excepţia punctelor şi că funcţia este continuă cu excepţia punctelor 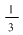 şi şi 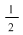 unde are discontinuităţi de prima speţă. unde are discontinuităţi de prima speţă.
Conform teoremei precedente, funcţia este integrabilă şi 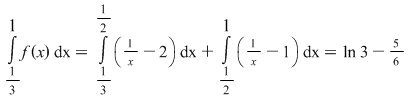 . .
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|