Functia exponentiala - definitie si grafic
Autor: Dana Schiopu
Descriere: articol pentru Clasa a X-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Functia exponentiala: definitie, exemple cu tabel de valori, convexitate, inegalitatea Jensen, exemple grafice.
Domenii: ---
FUNCŢIA EXPONENŢIALĂ
1.1. Importanţa studiului funcţiei exponenţiale constă în faptul că un număr mare de fenomene analizate de ştiinţe se exprimă cu ajutorul unei funcţii exponenţiale.
Definiţie:
Fie 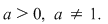 Funcţia Funcţia 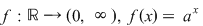 se numeşte funcţia exponenţială de bază se numeşte funcţia exponenţială de bază 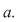
Observaţii:
1. Dacă 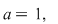 atunci funcţia atunci funcţia 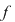 este definită pentru orice este definită pentru orice 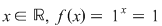 este constantă şi nu este considerată ca o funcţie exponenţială. este constantă şi nu este considerată ca o funcţie exponenţială.
2. A nu se confunda funcţia exponenţială 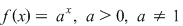 cu funcţia cu funcţia 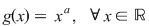
Dintre numerele 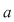 care pot fi baza unei funcţii exponenţiale merită menţionat numărul iraţional care pot fi baza unei funcţii exponenţiale merită menţionat numărul iraţional 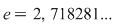 numit numărul lui Euler. numit numărul lui Euler.
Acest număr este important nu numai în matematică, dar şi în fizică şi alte ştiinţe ale naturii.
1.2. Graficul funcţiei exponenţiale.
Vom trasa graficul funcţiei exponenţiale în două cazuri:
1) baza 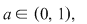 adică baza este subunitară adică baza este subunitară
2) baza 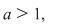 adică baza este supraunitară. Vom alege două valori ale bazei pentru a surprinde comportarea funcţiei atunci când baza este variabilă. adică baza este supraunitară. Vom alege două valori ale bazei pentru a surprinde comportarea funcţiei atunci când baza este variabilă.
1) Graficul funcţiei exponenţiale 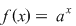 cu baza subunitară cu baza subunitară 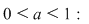
Vom considera funcţiile 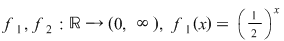 , , 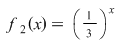 având bazele în relaţia: având bazele în relaţia: 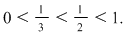
|