Functia exponentiala - proprietati
Autor: Dana Schiopu
Descriere: articol pentru Clasa a X-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Proprietati ale functiei exponentiale: exponentiala sumei este efala cu suma exponentialelor, convexitate, monotonie, injectivitate, surjectivitate.
Domenii: ---
Cum 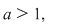 atunci atunci 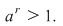 Din Din 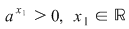 , deducem , deducem 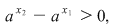 adică adică 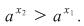
Analog se procedează dacă 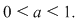
Observaţie:
Monotonia funcţiei exponenţiale intervine la rezolvarea inecuaţiilor exponenţiale.
Pentru 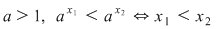
Pentru 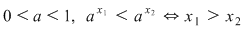
c. Funcţia exponenţială este convexă. Pentru funcţiile pe care le studiem noi, condiţia de convexitate este echivalentă cu inegalitatea lui Jensen.
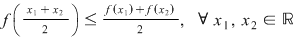 ceea ce este uşor de probat. ceea ce este uşor de probat.
Forma graficului arată că orice tangentă într-un punct al graficului lasă graficul deasupra tangentei.
Observaţie:
Funcţia exponenţială fiind convexă nu îşi poate atinge cea mai mare valoare în interiorul intervalului.
d. 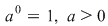
e. Funcţia exponenţială este bijectivă şi deci inversabilă.
Demonstraţie:
O funcţie este bijectivă dacă este atât injectivă cât şi surjectivă (admitem surjectivitatea fără demonstraţie).
Intuitiv, faptul că funcţia exponenţială este surjectivă se observă din graficul ei, iar din b. rezultă că 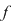 este injectivă, fiind o funcţie monotonă. Fiind bijectivă această funcţie este inversabilă. este injectivă, fiind o funcţie monotonă. Fiind bijectivă această funcţie este inversabilă.
Această proprietate ne permite să scriem echivalenţa:
 care va rezolva ecuaţiile exponeţiale. care va rezolva ecuaţiile exponeţiale.
|