Inversarea functiilor continue
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Teorema de caracterizare a functiilor cu proprietatea lui Darboux. Teorema valorilor intermediare. Exemple. Teorema: orice functie continua si injectiva pe un interval este strict monotona; orice functie continua pe un interval si surjectiva este bijectiva daca si numai daca este strict monotona; exemple.
Domenii: Functii continue
 INVERSAREA FUNCŢIILOR CONTINUE
INVERSAREA FUNCŢIILOR CONTINUE
Vom enunţa două teoreme ce au un rezultat important:
Teorema 1: O funcţie 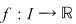 are proprietatea lui Darboux are proprietatea lui Darboux  imaginea oricărui interval prin imaginea oricărui interval prin 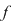 este tot un interval. este tot un interval.
Teorema 2: (a valorilor intermediare)
Orice funcţie continuă pe un interval are proprietatea lui Darboux pe acel interval.
Din aceste două teoreme se obţine următorul corolar:
Corolar : fie 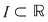 un interval şi un interval şi 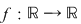 , o funcţie continuă pe , o funcţie continuă pe 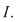 Mulţimea Mulţimea 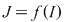 este tot un interval. este tot un interval.
Exemplu: Fie funcţia 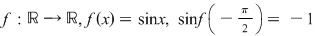 şi şi 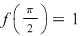 şi din continuitatea funcţiei şi din continuitatea funcţiei 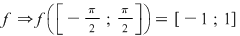 . .
Acest corolar ajută la demonstrarea riguroasă a surjectivităţii unor funcţii.
Consecinţă: Fie 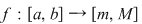 continuă pe continuă pe 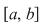 cu cu 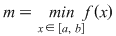 ; ; 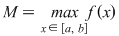 . .
Atunci 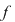 este surjectivă. este surjectivă.
În general, dacă marginile 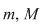 ale unei funcţii continue ale unei funcţii continue 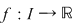 pe un interval pe un interval 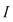 sunt atinse, atunci sunt atinse, atunci 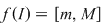 . Dacă niciuna din marginile funcţiei nu este atinsă, atunci . Dacă niciuna din marginile funcţiei nu este atinsă, atunci 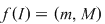 . (aici . (aici 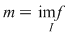 , , 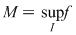 calculate în calculate în 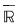 ) )
Exemplu: Pentru funcţia 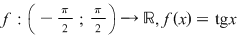 avem avem 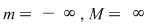 deci deci 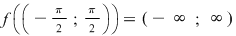 . .
Observaţie 1) Dacă 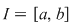 şi şi 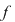 este continuă pe este continuă pe 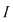 , nu rezultă în general că , nu rezultă în general că 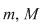 sunt atinse chiar în capetele intervalului sunt atinse chiar în capetele intervalului 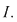
Observaţie 2) Daca 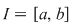 atunci pentru atunci pentru 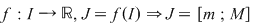
( 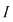 interval închis interval închis 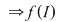 tot interval închis ). Dacă tot interval închis ). Dacă 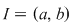 (interval deschis) despre (interval deschis) despre 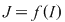 , cu , cu 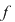 funcţie continuă nu se poate afirma decât faptul că este interval, fără a se putea specifica ce fel de interval este. Se poate întâmpla ca funcţie continuă nu se poate afirma decât faptul că este interval, fără a se putea specifica ce fel de interval este. Se poate întâmpla ca 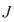 să fie nemărginit. să fie nemărginit.
Materiale Didactice Asemanatoare
 Functii cu proprietatea lui Darboux Functii cu proprietatea lui Darboux
|