Relatia dintre functii derivabile si functii continue
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 14 Mar 2008, nivel de dificultate  . .
O functie derivabila (intr-un punct) este continua (in acel punct), exemple.
Domenii: Functii derivabile
Relaţia dintre funcţii derivabile
şi funcţii continue
Teoremă: Orice funcţie derivabilă într-un punct este continuă în acel punct.
Demonstraţie:
Fie 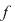 derivabilă în derivabilă în 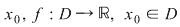
Fie 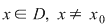
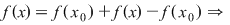
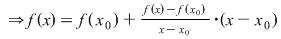
Dar 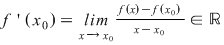 , deoarece , deoarece  este derivabilă în este derivabilă în  şi şi 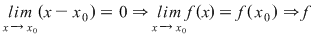 continuă în continuă în 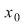 . .
Consecinţă: Dacă 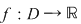 este o funcţie derivabilă pe este o funcţie derivabilă pe 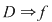 este continuă pe este continuă pe 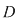 . .
Observaţie:
Reciproca nu este în general adevărată. Este posibil ca o funcţie să fie continuă într-un punct 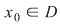 , fără să fie derivabilă în , fără să fie derivabilă în 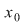 . .
Exemplu:
Funcţia 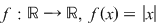
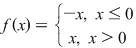
Se demonstrează continuitatea în 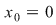
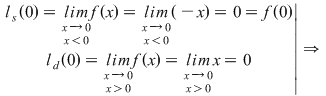
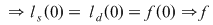 continuă în continuă în 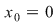 . .
Se verifică dacă 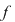 este derivabilă în este derivabilă în 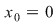
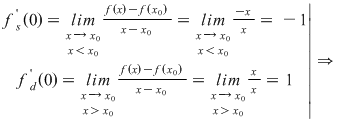
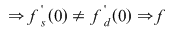 nu este derivabilă în nu este derivabilă în 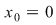 . .
Exemplu:
Fie 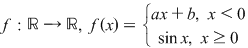
Determină 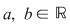 pentru care pentru care 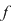 este derivabilă în este derivabilă în 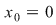 . .
Soluţie: 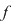 este derivabilă în este derivabilă în 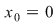
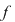 este continuă în este continuă în 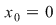
Din continuă în 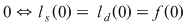
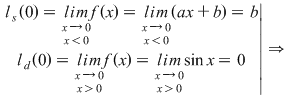
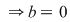
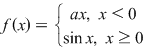
Se pune condiţia derivabilităţii în 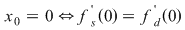
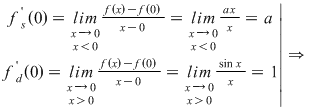
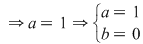
|