Sisteme de ecuatii liniare - cazul general
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XI-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Sisteme de ecuatii liniare: metoda Cramer, descriere; teorema lui Rouche, demonstratie. Exemple.
Domenii: Sisteme liniare
Sisteme de ecuaţii liniare - cazul general
Ne propunem discuţia şi rezolvarea unui sistem de 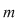 ecuaţii liniare cu ecuaţii liniare cu 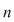 necunoscute necunoscute 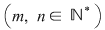 de forma: de forma:
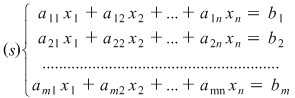 cu matricea asociată: cu matricea asociată:
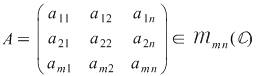
Precizăm că o soluţie a acestui sistem este un ansamblu de 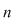 numere comlexe numere comlexe 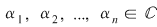 care verifică fiecare ecuaţie a sistemului. care verifică fiecare ecuaţie a sistemului.
Dacă un sistem are soluţii, atunci se numeşte compatibil (determinat - soluţie unică, nedeterminat - cel puţin două soluţii), iar dacă nu are soluţii se numeşte incompatibil.
Mijloacele pe care le avem la dispoziţie sunt două:
1) Formulele lui Cramer, care se aplică unui număr restrâns de sisteme (când 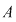 este pătratică şi nesingulară): este pătratică şi nesingulară):
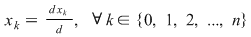 unde unde 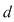 este determinantul matricii asociate sistemului şi este determinantul matricii asociate sistemului şi 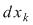 sunt determinanţii ce se obţin înlocuind coloana sunt determinanţii ce se obţin înlocuind coloana 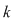 cu coloana termenilor liberi. cu coloana termenilor liberi.
2) Noţiunea de rang al unei matrice:
Dacă 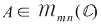 şi şi 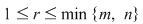 , atunci , atunci 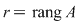 dacă există un minor de ordinul dacă există un minor de ordinul 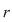 nenul şi toţi minorii de ordin nenul şi toţi minorii de ordin 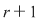 (dacă există) sunt nuli. (dacă există) sunt nuli.
Ideea de rezolvare a unui astfel de sistem este aceea de a-l "aşeza" sub o formă căreia să-i putem aplica formulele lui Cramer. Să presupunem că am determinat 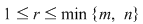 cu cu 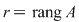 , adică există un minor de ordin nenul, fie acesta: , adică există un minor de ordin nenul, fie acesta:
|