 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
Soluţie:
Dacă în relaţia din enunţ luăm 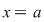 , , 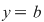 , obţinem , obţinem 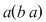 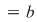 , ceea ce arată că , ceea ce arată că 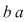 este soluţie a ecuaţiei este soluţie a ecuaţiei 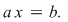 Să arătăm că această soluţie este unică. Să arătăm că această soluţie este unică.
Fie 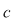 o soluţie arbitrară a ecuaţiei o soluţie arbitrară a ecuaţiei 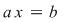 , adică , adică 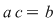 (1) (1)
Luând în condiţia din enunţ 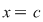 , , 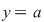 , obţinem , obţinem 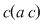 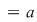 , adică folosim (1) , adică folosim (1)
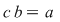 (2) (2)
Luăm acum în relaţia din enunţ 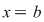 , , 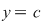 şi obţinem şi obţinem 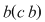 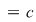 , adică conform cu (2), , adică conform cu (2), 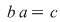 . .
Egalitatea 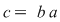 la care am ajuns arată că soluţia ecuaţiei la care am ajuns arată că soluţia ecuaţiei 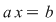 este unică. este unică.
Vom demonstra acum egalitatea:
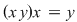 , , 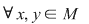 (3) (3)
(atenţie: operaţia nu este asociativă)
Dacă în relaţia din enunţ înlocuim pe 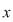 cu cu 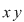 avem avem 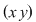 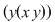 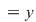 şi dacă ţinem seama că şi dacă ţinem seama că 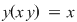 (tot datorită relaţiei din enunţ) am obţinut (tot datorită relaţiei din enunţ) am obţinut
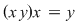 , adică (3). , adică (3).
Folosind (3) şi procedând analog cum am făcut pentru ecuaţia 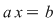 , se ajunge la concluzia că ecuaţia , se ajunge la concluzia că ecuaţia 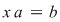 are drept unică soluţie pe are drept unică soluţie pe 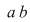 . .
Dăm acum un exemplu de mulţime 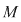 înzestrată cu o astfel de operaţie. Luăm înzestrată cu o astfel de operaţie. Luăm
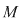
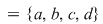 şi tabla operaţiei şi tabla operaţiei
| |
a |
b |
c |
d |
| a |
a |
d |
b |
c |
| b |
c |
b |
d |
a |
| c |
d |
a |
c |
b |
| d |
b |
c |
a |
d |
Această operaţie nu este asociativă, nu este comutativă şi nu admite element neutru.
VIII. Pentru fiecare 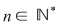 definim funcţia definim funcţia
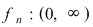 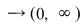 , , 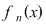 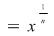 şi pentru fiecare şi pentru fiecare 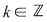 , definim funcţia , definim funcţia 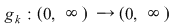 , , 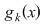 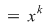 . .
Să se arate că:
a) Mulţimea 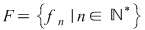 înzestrată cu operaţia de compunere este un monoid comutativ izomorf cu monoidul înzestrată cu operaţia de compunere este un monoid comutativ izomorf cu monoidul 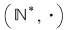 ; ;
b) Mulţimea 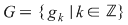 înzestrată cu operaţia de compunere este un monoid comutativ izomorf cu monoidul înzestrată cu operaţia de compunere este un monoid comutativ izomorf cu monoidul 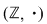 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|