Asupra unei teoreme Pick
Autor: Mihaela Badescu
Descriere: articol pentru Clasa a X-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Teorema de care ne vom ocupa în aceasta nota, cunoscuta sub numele de teorema lui Pick, permite calcularea ariei unui poligon din planul cartezian ale carui vârfuri au coordonate întregi. Rezultatul depinde doar de numarul de puncte de coordonate întregi din interiorul poligonului si de numarul de puncte de coordonate întregi care apartin poligonului.
Domenii: Elemente de geometrie analitica
Asupra unei teoreme a lui Pick
Rezultatul de care ne vom ocupa în această notă, cunoscut sub numele de teorema lui Pick, permite calcularea ariei unui poligon din planul cartezian ale cărui vârfuri au coordonate întregi (a se vedea [1], pag.68). Este un rezultat elegant şi, după cât se pare, puţin cunoscut la noi. Iată enunţul exact al teoremei lui Pick:
Teorema lui Pick [1]: Într-un sistem cartezian se consideră un poligon ale cărui vârfuri au coordonatele întregi. Atunci 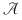 aria poligonului este dată de formula aria poligonului este dată de formula
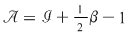 , unde , unde 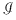 reprezintă numărul de puncte de coordonate întregi din interiorul poligonului, iar reprezintă numărul de puncte de coordonate întregi din interiorul poligonului, iar 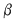 reprezintă numărul de puncte de coordonate întregi care aparţin poligonului. reprezintă numărul de puncte de coordonate întregi care aparţin poligonului.
Pentru a demonstra teorema lui Pick avem nevoie de următoarea:
Lemă: Teorema lui Pick este adevărată dacă poligonul este un triunghi oarecare sau un dreptunghi ale cărui laturi sunt paralele cu axele de coordonate.
Demonstraţia lemei. Cazul 1. Poligonul este un dreptunghi cu laturile paralele cu axele de coordonate. Dacă dreptunghiul, notat 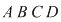 , conţine în interiorul laturii , conţine în interiorul laturii 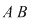 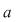 puncte de coordonate întregi şi puncte de coordonate întregi şi 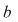 puncte de coordonate întregi în interiorul laturii puncte de coordonate întregi în interiorul laturii 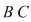 , atunci lungimea lui , atunci lungimea lui 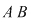 este egală cu este egală cu 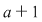 , lungimea laturii , lungimea laturii 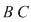 este este 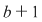 . Rezultă că aria dreptunghiului . Rezultă că aria dreptunghiului  este este 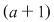 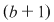 . În plus se obţine: . În plus se obţine:
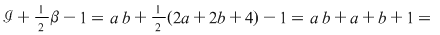
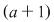 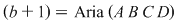 . .
Prin urmare formula este verificată în cazul unui dreptunghi (Fig.1).
Cazul 2. Poligonul este un triunghi  . Presupunem că laturile . Presupunem că laturile 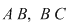 şi şi 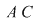 conţin conţin 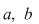 respectiv respectiv 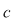 puncte de coordonate întregi, fără a considera capetele lor, şi interiorul triunghiului puncte de coordonate întregi, fără a considera capetele lor, şi interiorul triunghiului 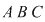 conţine conţine 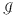 puncte de coordonate întregi. Se disting cinci poziţii ale triunghiului faţă de axele de coordonate: puncte de coordonate întregi. Se disting cinci poziţii ale triunghiului faţă de axele de coordonate:
a) Triunghiul 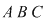 este dreptunghic şi are catetele paralele cu axele de coordonate (a se vedea Figura 1). este dreptunghic şi are catetele paralele cu axele de coordonate (a se vedea Figura 1).
Dreptunghiul 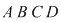 conţine conţine 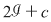 puncte interioare de coordonate întregi. Pentru triunghiul puncte interioare de coordonate întregi. Pentru triunghiul  avem: avem:
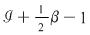 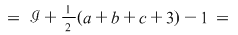
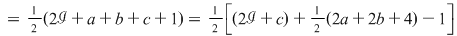
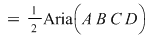 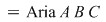 . .
În acest caz formula este verificată.
Bibliografie
| 1. Problem-solving through problems - Loren C. Larson - Editura: Springer-Verlag - New York, Berlin, Heidelberg, Tokyo (anul 1983) |
|