 Optiuni  Inapoi la biblioteca |
Despre continuitatea functiilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XI-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Continuitatea functiilor: scurt istoric. Punct de acumulare: definitie, exemple.Punct izolat, definitie, exemple. Definitii ale limitei unei functii intr-un punct. Definitia continuitatii unei functii intr-un punct,exemple, tipuri de probleme.
Domenii: ---
 Despre continuitatea funcţiilor
Despre continuitatea funcţiilor
 I. Enunţarea problemei I. Enunţarea problemei
În limbajul cotidian, spunem că o curbă este „continuă” dacă ea „nu are întreruperi”, iar dacă într-un punct se întrerupe spunem că în acel punct curba NU este continuă sau că este „discontinuă”.
În acest context, prin graficul unei funcţii reale de variabilă reală 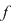 , înţelegem reprezentarea geometrică a acestui grafic sau curba reprezentativă a lui , înţelegem reprezentarea geometrică a acestui grafic sau curba reprezentativă a lui 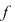 . .
Deoarece, în particular, curba poate fi graficul unei funcţii reale de variabilă reală, se pune problema să „transcriem” matematic această proprietate de continuitate a graficului funcţiei respective. Facem de la început precizarea că noţiunea de funcţie continuă (în mod paradoxal) a fost istoriceşte definită neaşteptat de târziu (A. Cauchy 1821), mult după ce fuseseră elaborate conceptele de derivată şi integrală si descoperite proprietăţile lor principale (Newton si Leibnitz - 1701). Prin urmare, trebuie subliniată dificultatea primară în prezentarea riguroasă a conceptului de continuitate, a cărui definiţie s-a impus doar în momentul fundamentării solide, logice a edificiului analizei matematice.
Mai precizăm că noţiunea de continuitate a unei funcţii într-un punct, asa cum vom arăta într-un exemplu simplu, este strâns legată de aceea de limită a unei funcţii într-un punct, motiv pentru care este necesar să reamintim:
a) Punct de acumulare : Dacă 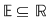 , atunci , atunci 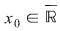 este un punct de acumulare al lui este un punct de acumulare al lui 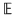 dacă: dacă: 
Mulţimea punctelor de acumulare ale lui 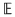 se notează cu se notează cu 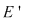 (mulţimea derivată a lui (mulţimea derivată a lui 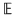 ) şi dacă ) şi dacă  , atunci: , atunci:
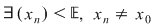 cu cu 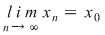
Exemple:
1). Dacă 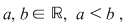 atunci orice punct de acumulare al intervalului atunci orice punct de acumulare al intervalului 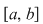 este punct de acumulare al intervalului este punct de acumulare al intervalului 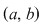 . .
2). Singurul punct de acumulare al lui 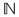 este este 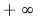 . .
3). Orice număr real este punct de acumulare al lui 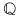 şi al lui şi al lui 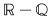 . .
b)Punct izolat: Spunem că 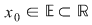 este punct izolat al lui este punct izolat al lui 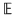 dacă există dacă există 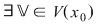 astfel încât astfel încât 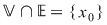
|