 Optiuni  Inapoi la biblioteca |
Despre continuitatea functiilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XI-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Continuitatea functiilor: scurt istoric. Punct de acumulare: definitie, exemple.Punct izolat, definitie, exemple. Definitii ale limitei unei functii intr-un punct. Definitia continuitatii unei functii intr-un punct,exemple, tipuri de probleme.
Domenii: ---
Exemple :
1) Orice punct al unei mulţimi finite este punct izolat al acestei mulţimi.
2) Orice punct al unei mulţimi care NU este punct de acumulare al unei mulţimi este punct izolat al acelei mulţimi.
3) Orice punct al mulţimii 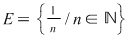 este punct izolat acesteia. este punct izolat acesteia.
4) Pentru mulţimea 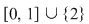 , elementul 2 este punct izolat. , elementul 2 este punct izolat.
5) Orice număr întreg este punct izolat al lui 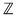 . .
În cazul definiţiei limitei unei funcţii 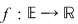 într-un punct într-un punct  se studiază comportarea lui se studiază comportarea lui 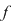 în jurul lui în jurul lui 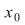 , valoarea lui , valoarea lui 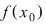 neluându-se în considerare şi ajungându-se la cele 3 definiţii echivalente. neluându-se în considerare şi ajungându-se la cele 3 definiţii echivalente.
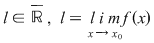 dacă şi numai dacă: dacă şi numai dacă:
I. Definiţia cu şiruri :
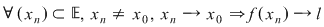
II. Definiţia cu vecinătăţi :
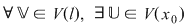 astfel încât astfel încât 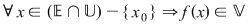
III. Definiţia cu 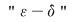 (dacă (dacă 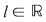 ): ):
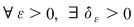 astfel încât astfel încât 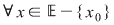 cu cu 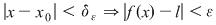
În plus, mai avem:
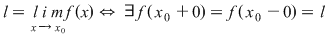
Problema care se pune acum pentru funcţia 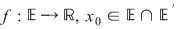 este dacă atunci când este dacă atunci când 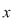 se apropie de se apropie de 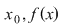 se apropie de se apropie de 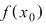 , PROBLEMĂ CARE ARE SENS numai dacă, în mod obligatoriu , , PROBLEMĂ CARE ARE SENS numai dacă, în mod obligatoriu , 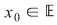
|