| |
 Optiuni  Inapoi la biblioteca |
Despre continuitatea functiilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XI-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Continuitatea functiilor: scurt istoric. Punct de acumulare: definitie, exemple.Punct izolat, definitie, exemple. Definitii ale limitei unei functii intr-un punct. Definitia continuitatii unei functii intr-un punct,exemple, tipuri de probleme.
Domenii: ---
II. Definiţia continuităţii unei funcţii într-un punct
Se poate pleca de la următorul exemplu:
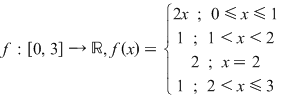
al cărei grafic este
Se vede că 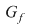 "se întrerupe" în 1 şi 2. "se întrerupe" în 1 şi 2.
Pentru 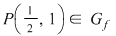 : : 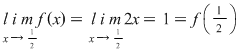
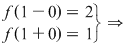 NU există NU există 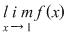
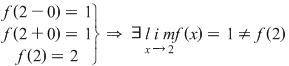
Aceste considerente ne conduc la următoarele :
DEF.1: 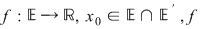 continuă în continuă în 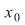 dacă şi numai dacă dacă şi numai dacă 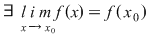  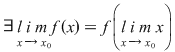
PRECIZĂRI:
a) Dacă 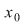 este un punct izolat al lui este un punct izolat al lui 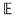 , atunci , atunci 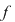 este continuă în este continuă în 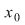 deoarece pentru: deoarece pentru:
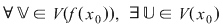 astfel încât astfel încât  şi şi 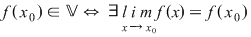
b) Nu se pune problema continuităţii într-un punct care NU este în domeniul de definiţie al funcţiei.
c) Dacă 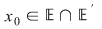 găsim: găsim:
f este continuă în 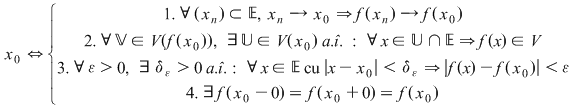
Dacă 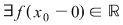 şi şi 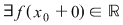 , dar , dar 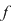 NU este continuă în NU este continuă în 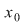 , atunci , atunci 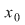 se numeşte punct de discontinuitate de prima speţă , iar punctele de discontinuitate care NU sunt de prima speţă se numesc puncte de discontinuitate de speţa a doua. se numeşte punct de discontinuitate de prima speţă , iar punctele de discontinuitate care NU sunt de prima speţă se numesc puncte de discontinuitate de speţa a doua.
|
| |
| |