Ecuatia exponentiala - partea I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a X-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Tipuri de ecuatii exponentiale, metode de rezolvare: logaritmare, exemple.
Domenii: Functia exponentiala, functia logaritm
Ecuaţii exponenţiale - Partea I
Prin ecuaţie exponenţială se înţelege o ecuaţie în care necunoscuta 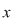 figurează la exponenţi. figurează la exponenţi.
Se numeşte soluţie a unei ecuaţii exponenţiale de necunoscută 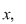 un număr real un număr real 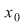 cu proprietatea că punând cu proprietatea că punând 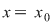 în ecuaţie, aceasta se verifică. în ecuaţie, aceasta se verifică.
A rezolva o ecuaţie exponenţială înseamnă a-i determina toate soluţiile. Rezolvarea ecuaţiilor exponenţiale se bazează pe proprietatea: două puteri de aceeaşi bază egale, au exponenţi egali.
Două ecuaţii exponenţiale se numesc echivalente dacă mulţimile de soluţii coincid.
1. Ecuaţii exponenţiale de forma:
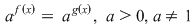
Metodă de rezolvare. Ecuaţia este echivalentă cu ecuaţia 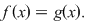 Soluţiile acestei ecuaţii sunt şi soluţii ale ecuaţiei date. Soluţiile acestei ecuaţii sunt şi soluţii ale ecuaţiei date.
Probleme:
Să se rezolve ecuaţiile:
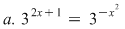
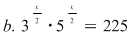
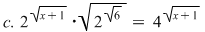
Soluţii:
a. Ecuaţia este echivalentă cu ecuaţia 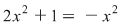 şi are soluţia dublă şi are soluţia dublă 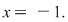
b. Ecuaţia se scrie echivalent 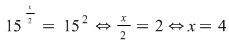
c. Necunoscuta figurează sub radical de ordin par, deci se impune condiţia 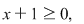 adică adică 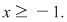
Materiale Didactice Asemanatoare
 Ecuatia exponentiala - partea II Ecuatia exponentiala - partea II
 Ecuatia exponentiala - partea III Ecuatia exponentiala - partea III
 Ecuatia exponentiala - partea IV Ecuatia exponentiala - partea IV
Bibliografie
| 1. Manual pentru clasa a X-a - Ganga M. - Editura: MathPress |
|