| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Ecuatia exponentiala - partea III
Autor: Dana Schiopu
Descriere: articol pentru Clasa a X-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Ecuatii exponentiale omogene. Ecuatii exponentiale cu baze diferite. Aplicatii.
Domenii: Functia exponentiala, functia logaritm
Punem 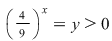 şi obţinem ecuaţia: şi obţinem ecuaţia:
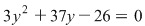 cu soluţiile cu soluţiile 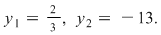
Cum 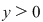 se reţine valoarea se reţine valoarea 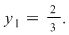
Se revine la substituţie şi se rezolvă ecuaţia:
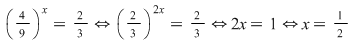
Deci soluţia ecuaţiei date este 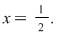
b. Ecuaţia se scrie echivalent.
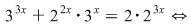
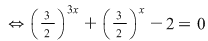
Fie 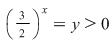 şi ultima ecuaţie devine şi ultima ecuaţie devine
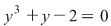 cu soluţia reală cu soluţia reală 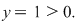
Deci 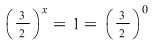 când când 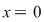
Ecuaţia dată are soluţia 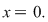
8. Ecuaţii care se rezolvă prin descompuneri în factori sau substituţii.
Metoda de rezolvare:
Pentru a rezolva ecuaţiile exponenţiale cu baze diferite, în general, se recomandă descompunerea bazelor în factori primi, observând o posibilitate de a grupa termenii ecuaţiei în ideea de a scrie ecuaţia ca un produs de factori egal cu 0. În alte cazuri se remarcă o anume expresie depinzând de necunoscuta care poate fi substituită şi se rescrie ecuaţia dată în funcţie de noua necunoscută.
Materiale Didactice Asemanatoare
 Ecuatia exponentiala - partea I Ecuatia exponentiala - partea I
 Ecuatia exponentiala - partea II Ecuatia exponentiala - partea II
 Ecuatia exponentiala - partea IV Ecuatia exponentiala - partea IV
Bibliografie
| 1. Manual pentru clasa a X-a - Ganga M. - Editura: MathPress |
|
| |
| |