 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Ecuatii algebrice de grad superior
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Teorema lui Bezout. Scurt istoric despre rezovarea ecuatiilor algebrice de grad 1-4. Teorema Abel-Ruffini si teorema d’Alembert-Gauss (teorema fundamentala a algebrei). Numere intregi negative, numere rationale, numere complexe ca radacini de ecuatii algebrice. Relatii intre radacini si coeficienti (relatiile lui Viete) cu exemple. Rezolvarea ecuatiilor binome. Exemple si figuri geometrice pentru gradele 3,4. Rezolvarea ecuatiilor bipatrate. Exemple.
Domenii: Polinoame
Ecuaţii algebrice de grad superior
I. Noţiuni pregătitoare
Definiţie: Fie 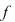 un polinom nenul cu coeficienţi complecşi. Un număr complex un polinom nenul cu coeficienţi complecşi. Un număr complex 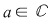 se numeşte rădăcină a polinomului se numeşte rădăcină a polinomului 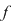 dacă dacă 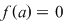 . .
Exemplu:
Fie polinomul 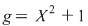 . Cum . Cum 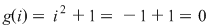 şi şi 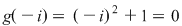 , rezultă că , rezultă că 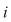 şi şi 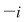 sunt rădăcini ale polinomului sunt rădăcini ale polinomului 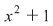 . .
Teorema lui Bezout: Fie 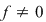 un polinom nenul. Numărul un polinom nenul. Numărul 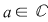 este rădăcină a polinomului este rădăcină a polinomului 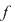 dacă şi numai dacă dacă şi numai dacă 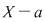 divide divide 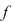 . .
Demonstraţie:
Dacă 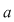 este rădăcină a lui este rădăcină a lui 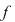 , adică , adică 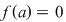 , atunci rezultă că restul împărţirii lui , atunci rezultă că restul împărţirii lui 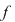 prin prin 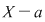 este zero şi deci este zero şi deci 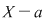 divide pe divide pe 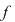 . Invers, dacă . Invers, dacă 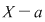 divide pe divide pe 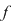 , atunci există un polinom , atunci există un polinom 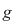 astfel încât astfel încât 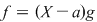 . Dar atunci . Dar atunci 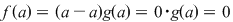 şi deci şi deci 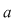 este rădăcină a lui este rădăcină a lui 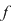 . .
II. Ecuaţii algebrice
Definiţie: Se numeşte ecuaţie algebrică de necunoscută 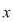 , o ecuaţie de forma , o ecuaţie de forma 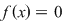 , unde , unde 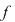 este un polinom nenul. este un polinom nenul.
Gradul polinomului 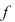 dă gradul ecuaţiei algebrice. Dacă dă gradul ecuaţiei algebrice. Dacă 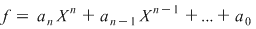 , , 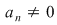 , atunci ecuaţia are gradul , atunci ecuaţia are gradul 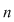 , iar coeficienţii , iar coeficienţii 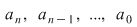 se numesc coeficienţii ecuaţiei algebrice. se numesc coeficienţii ecuaţiei algebrice.
Materiale Didactice Asemanatoare
 Aplicatii ale ecuatiilor algebrice de grad superior Aplicatii ale ecuatiilor algebrice de grad superior
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Soare N. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Elemente de Algebra - Ganga M. - Editura: MathPress |
|