 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Ecuatii algebrice de grad superior
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Teorema lui Bezout. Scurt istoric despre rezovarea ecuatiilor algebrice de grad 1-4. Teorema Abel-Ruffini si teorema d’Alembert-Gauss (teorema fundamentala a algebrei). Numere intregi negative, numere rationale, numere complexe ca radacini de ecuatii algebrice. Relatii intre radacini si coeficienti (relatiile lui Viete) cu exemple. Rezolvarea ecuatiilor binome. Exemple si figuri geometrice pentru gradele 3,4. Rezolvarea ecuatiilor bipatrate. Exemple.
Domenii: Polinoame
Dacă coeficienţii sunt numere reale, atunci ecuaţia algebrică se spune că este cu coeficienţi reali: dacă polinomul are coeficienţi raţionali, atunci ecuaţia se numeşte cu coeficienţi raţionali etc.
O ecuaţie care nu poate fi redusă la o ecuaţie algebrică prin operaţiile de: adunare, înmulţire, ridicare la putere etc., se numeşte ecuaţie transcendentă.
De exemplu: Ecuaţiile 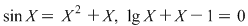 sunt ecuaţii transcendente. sunt ecuaţii transcendente.
Definiţie: Se spune că 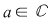 este soluţie (sau rădăcină) a ecuaţiei este soluţie (sau rădăcină) a ecuaţiei 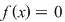 , dacă punând , dacă punând 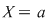 în ecuaţie, aceasta se verifică, adică în ecuaţie, aceasta se verifică, adică 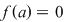 . .
Să observăm că dacă 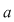 este rădăcină a ecuaţiei este rădăcină a ecuaţiei 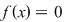 , atunci , atunci 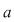 este rădăcină şi pentru polinomul este rădăcină şi pentru polinomul 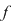 şi reciproc. Prin urmare, rezultatele stabilite pentru rădăcinile polinoamelor rămân valabile şi pentru ecuaţiile algebrice definite de acestea. şi reciproc. Prin urmare, rezultatele stabilite pentru rădăcinile polinoamelor rămân valabile şi pentru ecuaţiile algebrice definite de acestea.
A rezolva o ecuaţie algebrică înseamnă a-i determina soluţiile.
Pentru ecuaţiile de gradul întâi 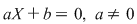 soluţia este soluţia este 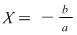 . Pentru ecuaţiile de gradul al doilea rădăcinile se calculează cu formulele: . Pentru ecuaţiile de gradul al doilea rădăcinile se calculează cu formulele:
a) 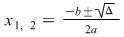 , unde , unde 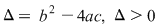
b) 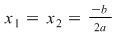 , unde , unde 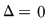
c) 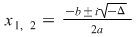 , daca , daca 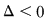 , unde ecuaţia are forma generală , unde ecuaţia are forma generală 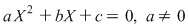 . .
Ecuaţiile algebrice de grad superior vor fi acele ecuaţii algebrice având gradul mai mare sau egal cu trei.
Încă din antichitate, matematicienii ştiau să determine rădăcinile ecuaţiilor algebrice de gradul I şi gradul II. În secolul al XVI-lea, în perioada Renaşterii italiene, matematicienii italieni Scipione del Ferro şi Niccolo Tartaglia au determinat formula de rezolvare pentru ecuaţia de gradul III, iar Ludovico Ferrari a determinat formula de rezolvare pentru ecuaţia de gradul IV. Acestea au fost publicate de Gerolamo Cardano în "Ars Magna" (1545).
Materiale Didactice Asemanatoare
 Aplicatii ale ecuatiilor algebrice de grad superior Aplicatii ale ecuatiilor algebrice de grad superior
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Soare N. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Elemente de Algebra - Ganga M. - Editura: MathPress |
|