Ecuatii algebrice de grad superior
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Teorema lui Bezout. Scurt istoric despre rezovarea ecuatiilor algebrice de grad 1-4. Teorema Abel-Ruffini si teorema d’Alembert-Gauss (teorema fundamentala a algebrei). Numere intregi negative, numere rationale, numere complexe ca radacini de ecuatii algebrice. Relatii intre radacini si coeficienti (relatiile lui Viete) cu exemple. Rezolvarea ecuatiilor binome. Exemple si figuri geometrice pentru gradele 3,4. Rezolvarea ecuatiilor bipatrate. Exemple.
Domenii: Polinoame
Încercările ulterioare ale matematicienilor de a găsi formule de rezolvare pentru ecuaţiile algebrice de grad mai mare decât patru au fost zadarnice. Problema a fost rezolvată de matematicianul norvegian Niels Henrik Abel şi de matematicianul italian Paolo Ruffini la începutul secolului al XIX-lea. Mai exact, ei au demonstrat:
Teorema Abel Ruffini: Ecuaţia algebrică generală de grad mai mare decât patru nu poate fi rezolvată prin radicali.
Vom vedea că există totuşi ecuaţii particulare de 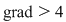 pentru care putem da formule de determinare a rădăcinilor lor. pentru care putem da formule de determinare a rădăcinilor lor.
Teorema fundamentală a algebrei:
Orice ecuaţie algebrică 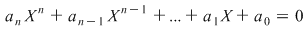 de grad mai mare sau egal cu de grad mai mare sau egal cu 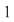 şi cu coeficienţi complecşi are cel puţin o rădăcină complexă. şi cu coeficienţi complecşi are cel puţin o rădăcină complexă.
Această teoremă mai poartă numele de teorema D'Alembert-Gauss. Nu vom da demonstraţiile teoremei fundamentale a algebrei şi a teoremei Abel-Ruffini, deoarece depăşesc cadrul lecţiei.
Trebuie să observăm că teorema fundamentală a algebrei are caracter existenţial; nicio demonstraţie a acestei teoreme nu ne indică vreun procedeu de obţinere a rădăcinilor ecuaţiilor algebrice. Acest lucru ne arată că nu există nici o contradicţie între cele două teoreme enunţate mai înainte.
Observaţie:
Din lecţiile precedente am văzut că lărgirea noţiunii de număr a fost impusă, printre altele, de rezolvarea anumitor ecuaţii. De exemplu, introducerea numerelor întregi a fost impusă de faptul că nu orice ecuaţie cu coeficienţi numere naturale are o rădăcină număr natural. De exemplu, ecuaţia 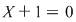 nu are nicio rădăcină număr natural. nu are nicio rădăcină număr natural.
Materiale Didactice Asemanatoare
 Aplicatii ale ecuatiilor algebrice de grad superior Aplicatii ale ecuatiilor algebrice de grad superior
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Soare N. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Elemente de Algebra - Ganga M. - Editura: MathPress |
|