 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Ecuatii algebrice de grad superior
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Teorema lui Bezout. Scurt istoric despre rezovarea ecuatiilor algebrice de grad 1-4. Teorema Abel-Ruffini si teorema d’Alembert-Gauss (teorema fundamentala a algebrei). Numere intregi negative, numere rationale, numere complexe ca radacini de ecuatii algebrice. Relatii intre radacini si coeficienti (relatiile lui Viete) cu exemple. Rezolvarea ecuatiilor binome. Exemple si figuri geometrice pentru gradele 3,4. Rezolvarea ecuatiilor bipatrate. Exemple.
Domenii: Polinoame
În continuare, introducerea numerelor raţionale a fost impusă de faptul că nu orice ecuaţie cu coeficienţi întregi are o rădăcină număr întreg. De exemplu, ecuaţia 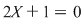 nu are nicio rădăcină număr întreg. nu are nicio rădăcină număr întreg.
Introducerea numerelor reale a fost impusă de faptul că nu orice ecuaţie cu coeficienţi raţionali are o rădăcină raţională. Nu avem de considerat decât ecuaţia 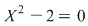 , care nu are nicio rădăcină raţională. , care nu are nicio rădăcină raţională.
Introducerea numerelor complexe, în algebră, a fost impusă de faptul că nu orice ecuaţie cu coeficienţi reali are o rădăcină reală. De exemplu, ecuaţia 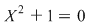 nu are nicio rădăcină reală. nu are nicio rădăcină reală.
Teorema lui D'Alembert-Gauss ne arată că procesul de lărgire pe această cale a noţiunii de număr se opreşte la numerele complexe.
III. Relaţii între rădăcini şi coeficienţi (formulele lui Viete)
Teoremă: Fie 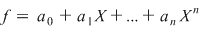 un polinom de grad un polinom de grad 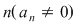 . Dacă . Dacă 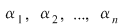 sunt rădăcinile lui sunt rădăcinile lui 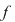 , atunci: , atunci:
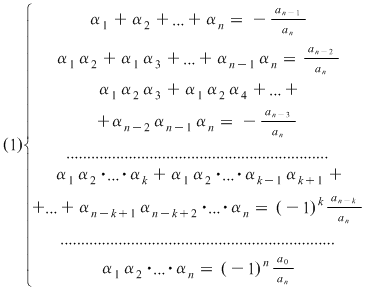
Materiale Didactice Asemanatoare
 Aplicatii ale ecuatiilor algebrice de grad superior Aplicatii ale ecuatiilor algebrice de grad superior
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Soare N. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Elemente de Algebra - Ganga M. - Editura: MathPress |
|