 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Ecuatii algebrice de grad superior
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Teorema lui Bezout. Scurt istoric despre rezovarea ecuatiilor algebrice de grad 1-4. Teorema Abel-Ruffini si teorema d’Alembert-Gauss (teorema fundamentala a algebrei). Numere intregi negative, numere rationale, numere complexe ca radacini de ecuatii algebrice. Relatii intre radacini si coeficienti (relatiile lui Viete) cu exemple. Rezolvarea ecuatiilor binome. Exemple si figuri geometrice pentru gradele 3,4. Rezolvarea ecuatiilor bipatrate. Exemple.
Domenii: Polinoame
Invers, dacă numerele complexe 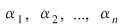 satisfac condiţiile de mai sus, atunci satisfac condiţiile de mai sus, atunci 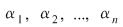 sunt rădăcinile polinomului sunt rădăcinile polinomului 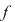 . .
Demonstraţie:
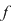 poate fi scris sub forma poate fi scris sub forma 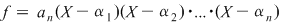 . Dar . Dar 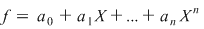 . .
Efectuând calculele şi egalând coeficienţii lui 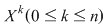 obţinem formulele din sistem. De exemplu, coeficientul lui obţinem formulele din sistem. De exemplu, coeficientul lui 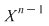 este este 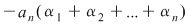 . Deci trebuie ca . Deci trebuie ca 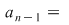 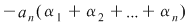 , de unde obţinem , de unde obţinem 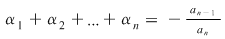 . În continuare, coeficientul lui . În continuare, coeficientul lui 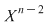 este este 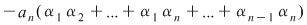 , care trebuie să fie egal cu , care trebuie să fie egal cu 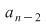 . Deci . Deci 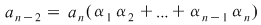 , de unde obţinem: , de unde obţinem:
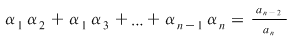
În acelaşi mod se obţin şi celelalte egalităţi.
Invers, presupunem că 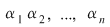 satisfac relaţiile din sistem. Considerăm polinomul satisfac relaţiile din sistem. Considerăm polinomul 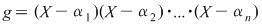 . Făcând înmulţirile, obţinem: . Făcând înmulţirile, obţinem:
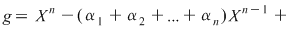
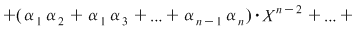
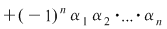 . .
Deducem că 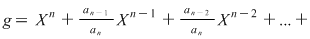
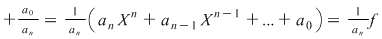
Din egalitatea 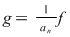 rezultă că rezultă că 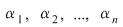 sunt rădăcini şi pentru sunt rădăcini şi pentru 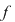 . .
Relaţiile 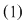 se numesc relaţiile lui Viete. se numesc relaţiile lui Viete.
Materiale Didactice Asemanatoare
 Aplicatii ale ecuatiilor algebrice de grad superior Aplicatii ale ecuatiilor algebrice de grad superior
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Soare N. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Elemente de Algebra - Ganga M. - Editura: MathPress |
|