Functii cu proprietatea lui Darboux
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietaea lui Darboux: definitie, teorema de caracterizare; teorema valorilor intermediare, exemplu.
Domenii: Functii continue
Grafic reprezentat acest rezultat :
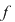 taie axa taie axa 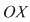 cel puţin o dată în intervalul cel puţin o dată în intervalul 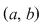 (are cel puţin un zero în acel interval). Lema anterioară ajută la demonstrarea unui rezultat important. (are cel puţin un zero în acel interval). Lema anterioară ajută la demonstrarea unui rezultat important.
Teorema 2 : (a valorilor intermediare)
Orice funcţie continuă pe un interval are proprietatea lui Darboux pe acel interval.
Demonstraţie. Fie 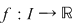 o funcţie continuă. Pentru a demonstra că o funcţie continuă. Pentru a demonstra că 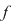 are proprietatea lui Darboux vom verifica definiţia. are proprietatea lui Darboux vom verifica definiţia.
Fie 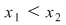 puncte oarecare din puncte oarecare din 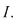
Fie 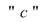 un număr situat între un număr situat între 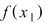 şi şi 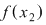 . Considerăm funcţia . Considerăm funcţia 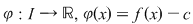
Deoarece 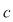 este între este între 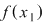 şi şi 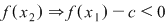 şi şi 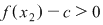 sau sau
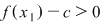 şi şi 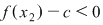
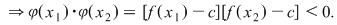
Conform lemei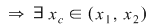 astfel încât astfel încât 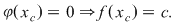
Astfel s-a verificat definiţia funcţiilor ce au proprietatea lui Darboux.
Observaţie. Reciproca teoremei valorilor intermediare nu este adevărată :
- există funcţii care au proprietatea lui Darboux pe un interval, dar care nu sunt continue pe acel interval.
Exemplu: Fie 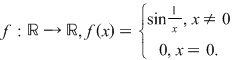
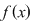 are proprietatea lui Darboux pe are proprietatea lui Darboux pe 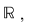 dar dar 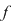 nu este continuă în nu este continuă în 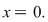
Materiale Didactice Asemanatoare
 Inversarea functiilor continue Inversarea functiilor continue
|