 Optiuni  Inapoi la biblioteca |
Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
2) Fie 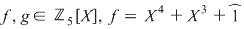 şi şi 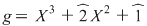 . Să arătăm că . Să arătăm că 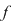 şi şi 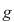 sunt prime între ele. Avem succesiv: sunt prime între ele. Avem succesiv:
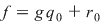 , unde , unde 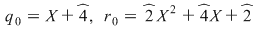
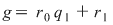 , unde , unde 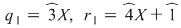
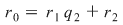 , unde , unde 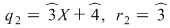
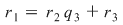 , unde , unde 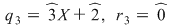
Deci 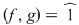
Avem 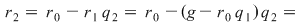
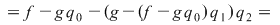
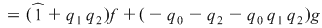 , deci , deci 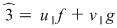 , unde , unde 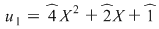 şi şi 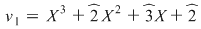 . Înmulţind ambii membri cu . Înmulţind ambii membri cu 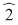 , obţinem , obţinem 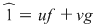 , unde , unde 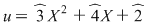 şi şi 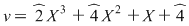 . .
(5.)
Rădăcinile unui polinom. Proprietăţi:
Fie 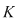 un corp comutativ şi un corp comutativ şi 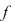 un polinom din un polinom din 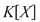 . Elementul . Elementul 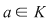 este o rădăcină a lui este o rădăcină a lui 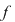 dacă dacă 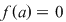 . .
Teorema 9: Fie 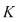 un corp comutativ, un corp comutativ, 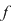 un polinom din un polinom din 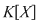 şi şi 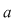 un element din un element din 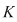 . Atunci există un unic polinom . Atunci există un unic polinom 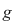 din din 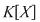 astfel încât astfel încât 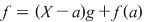 . .
Demonstraţie:
Din teorema împărţirii cu rest rezultă că există 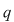 şi şi 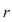 din din 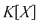 , unice, astfel încât , unice, astfel încât 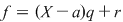 , unde , unde 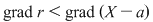 . Cum . Cum 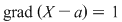 , rezultă , rezultă 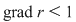 . Deci . Deci 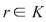 şi şi 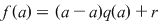 , de unde , de unde 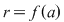 . Aşadar, . Aşadar, 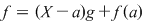 . .
Corolar: (Teorema lui Bezout). Fie 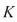 un corp comutativ şi un corp comutativ şi 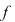 un polinom din un polinom din 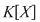 . Elementul . Elementul 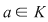 este o rădăcină a lui este o rădăcină a lui 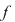 dacă şi numai dacă dacă şi numai dacă 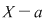 divide divide 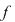 . .
SCHEMA LUI HORNER:
Fie 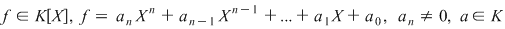 . Teorema împărţirii cu rest a lui . Teorema împărţirii cu rest a lui 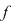 la la 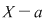 se scrie: se scrie: 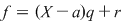 , unde câtul , unde câtul 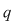 este un polinom de grad este un polinom de grad 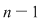 , iar restul , iar restul 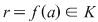 . .
Dacă 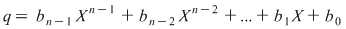 , atunci , atunci 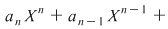
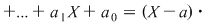
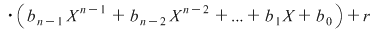 , de unde: , de unde: 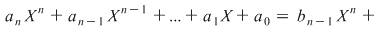
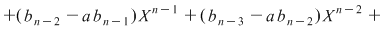
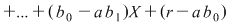 . .
|