Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
Din egalitatea celor două polinoame obţinem că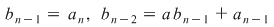 , ,
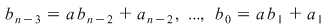
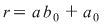 . .
Egalităţile se trec în tabelul următor:
Organizarea calculelor ca în tabelul de mai sus se numeşte schema lui Horner. Coeficienţii câtului se determină astfel: mai întâi coeficientul termenului de grad maxim 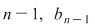 care este egal cu care este egal cu 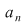 , apoi coeficientul termenului de grad , apoi coeficientul termenului de grad 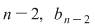 care este egal cu care este egal cu 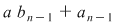 etc. etc.
Exemple:
1) Fie 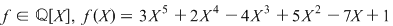
Să se determine câtul şi restul împărţirii polinomului 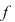 prin polinomul prin polinomul 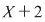 . Avem . Avem 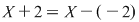 . .
Folosind schema lui Horner, obţinem:
Deci câtul este 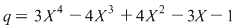 , iar restul este , iar restul este 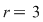 . .
2) Fie 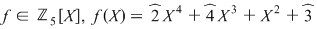 . Să se determine câtul şi restul împărţirii polinomului . Să se determine câtul şi restul împărţirii polinomului 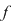 prin prin 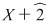 . .
Avem 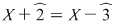 . Folosim schema lui Horner: . Folosim schema lui Horner:
Deci câtul este 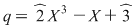 , iar restul este , iar restul este 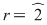 . .
|