 Optiuni  Inapoi la biblioteca |
Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
Fie 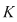 un corp comutativ, un corp comutativ, 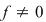 un polinom din un polinom din 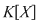 şi şi 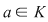 . Dacă . Dacă 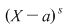 , unde , unde 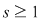 , divide pe , divide pe  în în 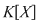 , atunci există un polinom , atunci există un polinom 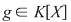 , unic determinat, astfel încât , unic determinat, astfel încât 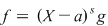 . .
Definiţie: Fie 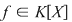 un polinom nenul şi un polinom nenul şi 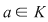 o rădăcină a lui o rădăcină a lui 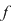 . Numărul . Numărul 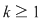 astfel încât astfel încât 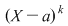 divide divide 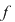 , iar , iar 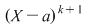 nu divide pe nu divide pe 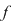 se numeşte ordinul de multiplicitate al rădăcinii se numeşte ordinul de multiplicitate al rădăcinii 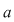 . Se mai spune că . Se mai spune că 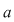 este o rădăcină multiplă de ordin este o rădăcină multiplă de ordin 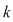 a lui a lui 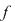 . .
Teorema 10: Fie 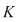 un corp şi un corp şi 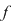 un polinom nenul din un polinom nenul din 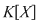 . Dacă . Dacă 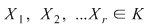 sunt rădăcini distincte ale lui sunt rădăcini distincte ale lui 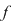 , având ordinele de multiplicitate respectiv , având ordinele de multiplicitate respectiv 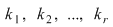 , atunci polinomul , atunci polinomul 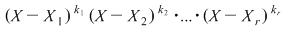 divide pe divide pe 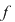 . .
Demonstraţie:
Procedăm prin inducţie după 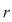 . Pentru . Pentru 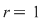 , teorema rezultă din definiţia de mai sus. Presupunem că ea este adevărată pentru , teorema rezultă din definiţia de mai sus. Presupunem că ea este adevărată pentru 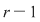 şi să demonstrăm pentru şi să demonstrăm pentru 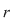 . Din ipoteza de inducţie, polinomul . Din ipoteza de inducţie, polinomul 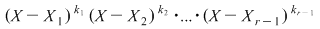 divide pe divide pe 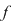 , adică există , adică există 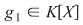 astfel încât: astfel încât: 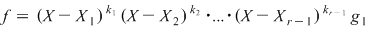 . .
Atunci 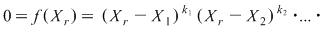
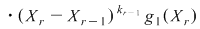 şi cum şi cum 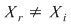 pentru orice pentru orice 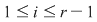 , rezultă , rezultă 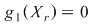 . .
Notând 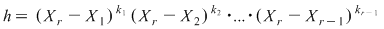 avem avem 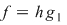 cu cu 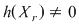 . Deoarece . Deoarece 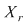 este rădăcină a lui este rădăcină a lui 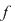 de ordin de multiplicitate de ordin de multiplicitate 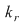 , rezultă că , rezultă că 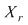 este rădăcină a lui este rădăcină a lui 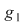 de acelaşi ordin de multiplicitate. Într-adevăr, cum de acelaşi ordin de multiplicitate. Într-adevăr, cum 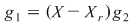 şi şi 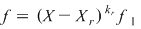 cu cu 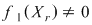 , înlocuind obţinem , înlocuind obţinem 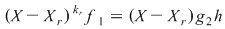 .Simplificând cu .Simplificând cu 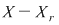 rezultă rezultă 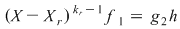 , de unde , de unde 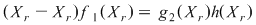 , adică , adică 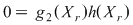 . Cum . Cum 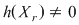 , atunci , atunci 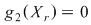 şi deci şi deci 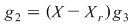 , unde , unde 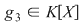 . Rezultă că . Rezultă că 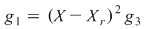 şi continuând procedeul de atâtea ori cât este ordinul de multiplicitate al rădăcinii şi continuând procedeul de atâtea ori cât este ordinul de multiplicitate al rădăcinii 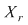 a lui a lui 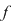 , obţinem , obţinem 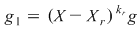 . Deci . Deci 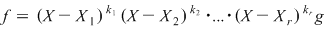 , unde , unde 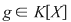 , adică , adică 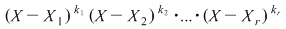 divide pe divide pe 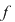 . .
|