 Optiuni  Inapoi la biblioteca |
Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
Soluţie: Restul împărţirii lui 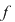 la la 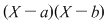 este un polinom de grad mai mic ca este un polinom de grad mai mic ca 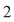 , fie acesta , fie acesta 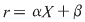 . Atunci teorema împărţirii cu rest a lui . Atunci teorema împărţirii cu rest a lui 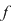 prin prin 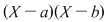 se scrie se scrie 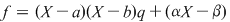 , unde , unde 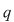 este câtul.Atunci este câtul.Atunci 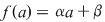 şi şi 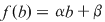 , unde , unde 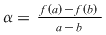 şi şi 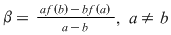 . Deci . Deci 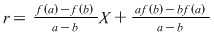 . De aici rezultă că dacă . De aici rezultă că dacă 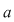 şi şi 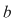 sunt două rădăcini distincte ale lui sunt două rădăcini distincte ale lui 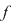 , atunci polinomul , atunci polinomul 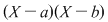 divide divide 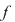 . .
2. Fie 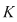 un corp comutativ infinit (de exemplu un corp comutativ infinit (de exemplu 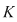 poate fi poate fi 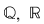 sau sau 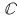 ), ), 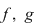 polinoame din polinoame din 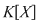 şi şi 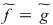 funcţiile polinomiale asociate. Atunci funcţiile polinomiale asociate. Atunci 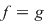 dacă şi numai dacă dacă şi numai dacă 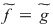 . .
Soluţie: Dacă 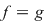 este clar că este clar că 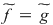 . Fie acum . Fie acum 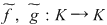 astfel încât astfel încât 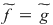 . Dacă . Dacă 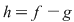 , atunci , atunci 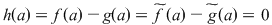 , oricare ar fi , oricare ar fi 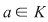 . Deoarece . Deoarece 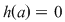 , oricare , oricare 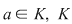 fiind infinit, din corolarul precedent rezultă fiind infinit, din corolarul precedent rezultă 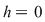 , adică , adică 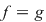 . .
3. (Teorema lui Wilson).
Dacă 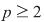 este un număr prim, atunci este un număr prim, atunci 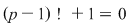 (modp). (modp).
Soluţie: Fie corpul 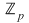 şi polinomul şi polinomul 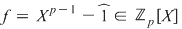 . Cum pentru orice . Cum pentru orice 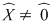 din din 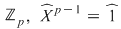 , rezultă că rădăcinile polinomului , rezultă că rădăcinile polinomului 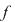 sunt sunt 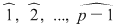 . Conform corolarului precedent, avem . Conform corolarului precedent, avem 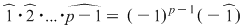 . Cum . Cum 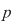 este prim, dacă este prim, dacă 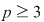 , atunci , atunci 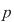 este impar şi deci este impar şi deci 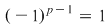 , iar , iar 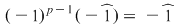 . Dacă . Dacă 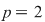 , atunci , atunci 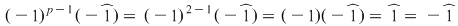 . Prin urmare, . Prin urmare, 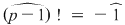 , de unde , de unde 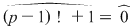 , adică , adică 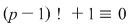 (modp). (modp).
|