Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
Teorema 4: Fie 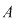 un domeniu de integritate. Atunci elementele inversabile ale inelului un domeniu de integritate. Atunci elementele inversabile ale inelului 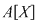 coincid cu elementele inversabile ale inelului coincid cu elementele inversabile ale inelului 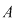 , adică , adică 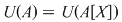 . .
Demonstraţie: Fie 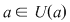 , adică există , adică există 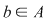 astfel încât astfel încât 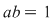 . Această relaţie are loc şi în . Această relaţie are loc şi în 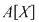 , , 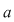 şi şi 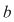 fiind polinoame de grad zero, şi deci, fiind polinoame de grad zero, şi deci, 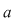 este inversabil în este inversabil în 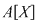 . .
Invers, fie 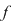 un polinom inversabil din un polinom inversabil din 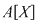 şi şi 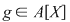 astfel încât astfel încât 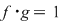 . Atunci . Atunci 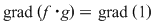 , adică , adică 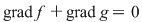 , de unde , de unde 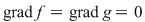 . Deci . Deci 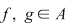 şi şi 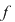 este inversabil în este inversabil în 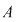 . .
Exemple:
1) 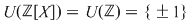
2) Pentru un corp comutativ 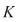 , avem , avem 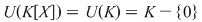 . Cu alte cuvinte, polinoamele inversabile din . Cu alte cuvinte, polinoamele inversabile din 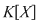 sunt polinoamele de grad zero şi numai acestea. sunt polinoamele de grad zero şi numai acestea.
(2.) Valoarea unui polinom. Funcţie polinomială.
Fie 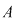 un inel comutativ şi un inel comutativ şi 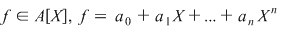 un polinom oarecare. Pentru un polinom oarecare. Pentru 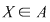 , punem , punem 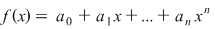 . Atunci . Atunci 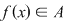 , iar , iar 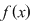 se numeşte valoarea polinomului se numeşte valoarea polinomului 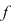 în în 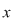 . Dacă . Dacă 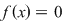 se spune că elementul se spune că elementul 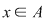 anulează polinomul anulează polinomul 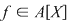 sau că sau că 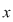 este o rădăcină a lui este o rădăcină a lui 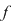 . .
Teorema 5: Fie 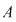 un inel comutativ, iar un inel comutativ, iar 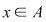 un element oarecare. Atunci oricare ar fi polinoamele un element oarecare. Atunci oricare ar fi polinoamele 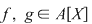 , avem: , avem: 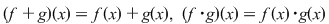 . .
Demonstraţie:
Fie 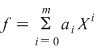 şi şi 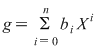 şi să presupunem că şi să presupunem că 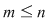 . Completând eventual polinomul . Completând eventual polinomul  cu termeni ai căror coeficienţi sunt zero, putem scrie cu termeni ai căror coeficienţi sunt zero, putem scrie 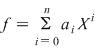 , unde , unde 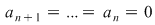 . Atunci, pentru . Atunci, pentru 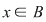 avem avem 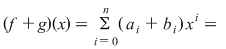
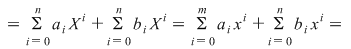
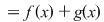 . Dacă notăm cu . Dacă notăm cu 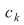 coeficienţii produsului coeficienţii produsului 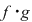 , avem , avem 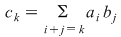 şi deci şi deci 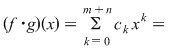
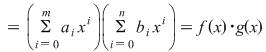 . În suma . În suma 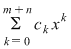 am scris şi termenii care eventual sunt zero. am scris şi termenii care eventual sunt zero.
|