 Optiuni  Inapoi la biblioteca |
Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
Dacă 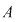 este un inel comutativ, iar este un inel comutativ, iar 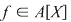 un polinom arbitrar, putem defini funcţia un polinom arbitrar, putem defini funcţia 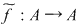 prin prin 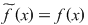 , oricare ar fi , oricare ar fi 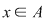 . Funcţia . Funcţia 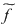 se numeşte funcţia polinomială asociată polinomului se numeşte funcţia polinomială asociată polinomului 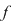 . .
Orice funcţie de la 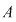 la la 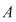 , care poate fi pusă sub forma unei funcţii , care poate fi pusă sub forma unei funcţii 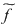 pentru un anumit pentru un anumit 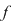 din din 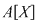 se numeşte funcţie polinomială pe se numeşte funcţie polinomială pe 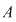 . Cea mai mare parte a funcţiilor de la . Cea mai mare parte a funcţiilor de la 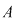 la la 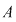 nu sunt funcţii polinomiale. De exemplu, dacă nu sunt funcţii polinomiale. De exemplu, dacă 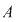 este corpul numerelor reale este corpul numerelor reale 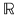 , funcţia modul , funcţia modul 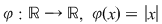 pentru orice pentru orice 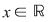 , nu este funcţie polinomială, deoarece , nu este funcţie polinomială, deoarece 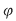 nu este derivabilă în zero, iar orice funcţie polinomială este indefinit derivabilă. nu este derivabilă în zero, iar orice funcţie polinomială este indefinit derivabilă.
Dacă 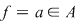 , atunci funcţia , atunci funcţia 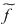 este constantă, este constantă, 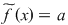 pentru orice pentru orice 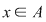 . De aceea, elementele inelului . De aceea, elementele inelului 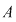 considerate ca polinoame se numesc polinoame constante. considerate ca polinoame se numesc polinoame constante.
Pot fi funcţii polinomiale 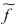 care să fie constante, chiar când care să fie constante, chiar când 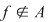 , dar numai acele polinoame care aparţin lui , dar numai acele polinoame care aparţin lui 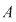 se numesc constante. se numesc constante.
De exemplu, fie inelul 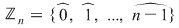 al claselor de resturi modulo al claselor de resturi modulo 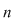 . Dacă . Dacă 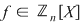 este polinomul este polinomul 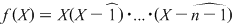 , avem , avem 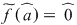 , oricare ar fi , oricare ar fi 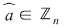 , dar , dar 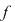 nu este polinom constant. nu este polinom constant.
(3.)
Teorema împărţirii cu rest.
Fie 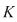 un corp comutativ. De exemplu, corpul un corp comutativ. De exemplu, corpul 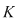 poate fi oricare dintre corpurile de numere poate fi oricare dintre corpurile de numere 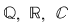 , sau corpul , sau corpul 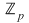 , cu , cu 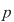 număr prim. Vom arăta că proprietăţi similare are orice inel de polinoame număr prim. Vom arăta că proprietăţi similare are orice inel de polinoame 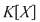 , unde , unde 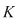 este un corp comutativ oarecare. este un corp comutativ oarecare.
Teorema 6: (teorema împărţirii cu rest). Fie 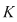 un corp comutativ, iar un corp comutativ, iar 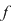 şi şi 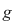 , cu , cu 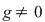 , polinoame din , polinoame din 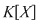 . Atunci există polinoamele . Atunci există polinoamele 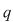 şi şi 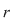 din din 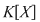 , unic determinate, astfel încât , unic determinate, astfel încât 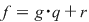 cu cu 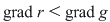 . .
Polinoamele 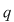 şi şi 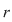 se numesc câtul şi respectiv restul împărţirii lui se numesc câtul şi respectiv restul împărţirii lui 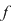 prin prin 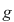 . .
Demonstraţie:
Vom arăta mai întâi existenţa polinoamelor 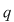 şi şi 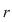 . Procedăm prin inducţie după gradul lui . Procedăm prin inducţie după gradul lui 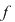 . Fie . Fie 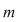 gradul lui gradul lui 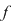 şi şi 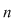 gradul lui gradul lui 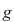 . Dacă . Dacă 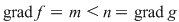 , luăm , luăm 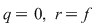 şi avem şi avem 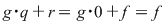 cu cu 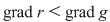 . Dacă . Dacă 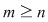 , fie , fie 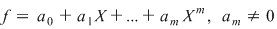 şi şi 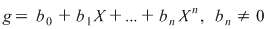 . Cum . Cum 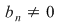 , iar , iar 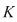 este corp, rezultă că este corp, rezultă că 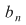 este inversabil. Considerăm polinomul este inversabil. Considerăm polinomul 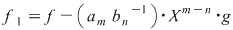 cu coeficienţi în cu coeficienţi în 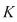 . Deoarece coeficienţii lui . Deoarece coeficienţii lui 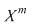 în în 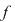 şi în şi în 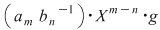 sunt egali, rezultă că sunt egali, rezultă că 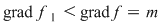 . .
|