Sisteme de ecuatii de gradul I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a IX-a publicat in data de 09 Iul 2008, nivel de dificultate  . .
Sisteme liniare de doua ecuatii cu doua necunoscute. Interpretare geometrica. Sisteme echivalente, transformari. Metode de rezvolvare: metoda reducerii, metoda substitutiei. Aplicatii. Probleme care se rezolva cu ajutorul sistemelor.
Domenii: ---
SISTEME DE ECUAŢII DE GRADUL ÎNTÂI DE FORMA 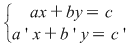
Definiţie:
Se numeşte ecuaţie de gradul întâi cu două necunoscute 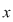 şi şi 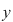 o ecuaţie de forma o ecuaţie de forma 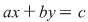 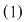 , unde , unde 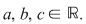
Numerele 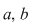 se numesc coeficienţii necunoscutelor se numesc coeficienţii necunoscutelor 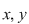 iar iar 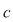 este termenul liber al ecuaţiei este termenul liber al ecuaţiei 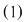 . Se numeşte soluţie a ecuaţiei . Se numeşte soluţie a ecuaţiei 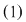 orice cuplu orice cuplu 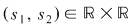 care verifică egalitatea care verifică egalitatea 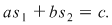
O ecuaţie de forma 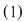 se mai numeşte ecuaţie liniară în se mai numeşte ecuaţie liniară în 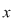 şi şi 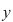 . Pentru soluţia . Pentru soluţia 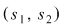 a ecuaţiei a ecuaţiei 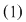 vom scrie vom scrie 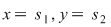 . .
Pentru a obţine soluţia generală a ecuaţiei 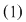 se pune se pune 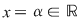 şi obţinem pentru şi obţinem pentru 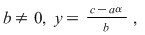 adică adică 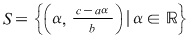
Mulţimea punctelor din plan care are coordonatele din 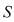 reprezintă o dreaptă de ecuaţie reprezintă o dreaptă de ecuaţie 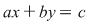 . Dacă . Dacă 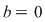 , atunci ecuaţia , atunci ecuaţia 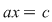 are soluţia are soluţia 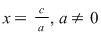 . În planul raportat la un reper cartezian, ecuaţia . În planul raportat la un reper cartezian, ecuaţia 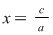 , reprezintă o dreaptă paralelă cu , reprezintă o dreaptă paralelă cu 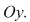
Exemplu:
Ecuaţia 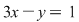 are coeficienţii are coeficienţii 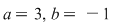 , iar temenul liber , iar temenul liber 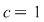 . O soluţie a ecuaţie este . O soluţie a ecuaţie este 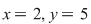 , iar soluţia generală a ecuaţiei este , iar soluţia generală a ecuaţiei este 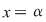 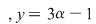 , ,
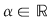 . .
Definiţie:
Un sistem de două ecuaţii de gradul întâi (sau încă sistem liniar) cu două necunoscute 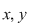 are forma are forma 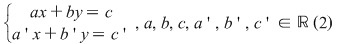
|