Sisteme de ecuatii de gradul I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a IX-a publicat in data de 09 Iul 2008, nivel de dificultate  . .
Sisteme liniare de doua ecuatii cu doua necunoscute. Interpretare geometrica. Sisteme echivalente, transformari. Metode de rezvolvare: metoda reducerii, metoda substitutiei. Aplicatii. Probleme care se rezolva cu ajutorul sistemelor.
Domenii: ---
Numerele 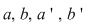 se numesc coeficienţii necunoscutelor, iar numerele se numesc coeficienţii necunoscutelor, iar numerele 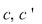 se numesc termenii liberi ai sistemului se numesc termenii liberi ai sistemului 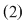 . .
Dacă 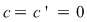 sistemul se numeşte liniar omogen. sistemul se numeşte liniar omogen.
Se numeşte soluţie a sistemului 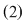 orice cuplu orice cuplu 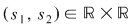 care este soluţie pentru fiecare din ecuaţiile sistemului. care este soluţie pentru fiecare din ecuaţiile sistemului.
Pentru sistemul liniar omogen cuplul 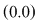 este întotdeauna soluţie (numită banală). este întotdeauna soluţie (numită banală).
A rezolva sistemul 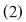 înseamnă a-i determina soluţiile (dacă există). înseamnă a-i determina soluţiile (dacă există).
Spunem că sistemul 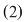 este: este:
1) Compatibil determinat dacă are o unică soluţie.
2) Compatibil nedeterminat dacă are mai mult de o soluţie.
3) Incompatibil dacă nu are soluţii.
Interpretarea geometrică a acestui fapt algebric este următoarea: în planul cartezian reprezentarea grafică a soluţiilor ecuaţiilor din 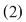 sunt două drepte de ecuaţii: sunt două drepte de ecuaţii:
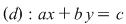
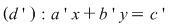
Dacă sistemul 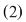 este compatibil determinat având soluţia este compatibil determinat având soluţia 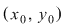 înseamnă că punctul înseamnă că punctul 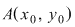 din plan se află pe fiecare din dreptele din plan se află pe fiecare din dreptele 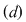 şi şi 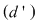 . Deci . Deci 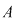 este punctul de intersecţie al acestor două drepte. este punctul de intersecţie al acestor două drepte.
Aşadar: pentru a obţine punctul de intersecţie a două drepte concurente se rezolvă sistemul format din ecuaţiile celor două drepte.
Dacă sistemul 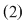 este compatibil nedeterminat înseamnă că mai mult de două puncte având coordonatele din mulţimea este compatibil nedeterminat înseamnă că mai mult de două puncte având coordonatele din mulţimea 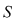 a soluţiilor sistemului se află pe cele două drepte. Cum două puncte distincte determină o unică dreaptă deducem că dreptele a soluţiilor sistemului se află pe cele două drepte. Cum două puncte distincte determină o unică dreaptă deducem că dreptele 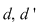 coincid, adică coincid, adică
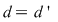 . .
În fine când sistemul 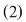 este incompatibil, situaţia corespunde în planul cartezian cu faptul că dreptele n-au puncte comune, adică sunt paralele. Deci este incompatibil, situaţia corespunde în planul cartezian cu faptul că dreptele n-au puncte comune, adică sunt paralele. Deci 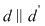 . .
|