Sisteme de ecuatii de gradul I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a IX-a publicat in data de 09 Iul 2008, nivel de dificultate  . .
Sisteme liniare de doua ecuatii cu doua necunoscute. Interpretare geometrica. Sisteme echivalente, transformari. Metode de rezvolvare: metoda reducerii, metoda substitutiei. Aplicatii. Probleme care se rezolva cu ajutorul sistemelor.
Domenii: ---
Sisteme echivalente
Două sisteme de ecuaţii de forma 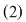 sunt echivalente dacă mulţimile de soluţii ale lor sunt egale. sunt echivalente dacă mulţimile de soluţii ale lor sunt egale.
Ca şi în cazul rezolvării ecuaţiilor şi pentru rezolvarea sistemelor de forma 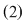 vom utiliza transformări care le fac echivalente cu alte sisteme mai simple de rezolvat. vom utiliza transformări care le fac echivalente cu alte sisteme mai simple de rezolvat.
 TRANSFORMĂRI ALE ECUAŢIILOR UNUI SISTEM
TRANSFORMĂRI ALE ECUAŢIILOR UNUI SISTEM
Fie sistemul 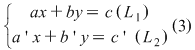 , unde am notat , unde am notat 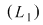 , , 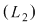 prima şi respectiv a doua ecuaţie. prima şi respectiv a doua ecuaţie.
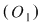 Adunarea unei ecuaţii a sistemului la o altă ecuaţie a sistemului. Adunarea unei ecuaţii a sistemului la o altă ecuaţie a sistemului.
Prin adunarea, membru cu membru, a celor două ecuaţii rezultă ecuaţia notată 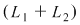 : : 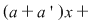 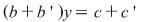 . .
Să observăm că orice soluţie 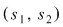 a sistemului a sistemului 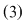 verifică şi ecuaţia verifică şi ecuaţia 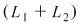 . .
Într-adevăr avem: 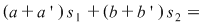
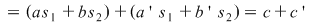
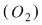 Înmulţirea ecuaţiilor sistemului prin factori nenuli. Înmulţirea ecuaţiilor sistemului prin factori nenuli.
Înmulţind ecuaţia 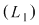 prin prin 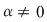 se obţine ecuaţia notată se obţine ecuaţia notată 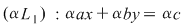
Orice soluţie 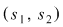 a sistemului a sistemului 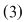 este soluţie şi pentru ecuaţia este soluţie şi pentru ecuaţia 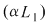 . .
Avem 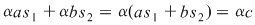
Observaţie:
Se pot combina cele două operaţii pentru a obţine ecuaţia 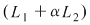 . .
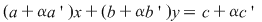 , pentru care orice soluţie , pentru care orice soluţie 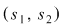 a sistemului a sistemului 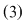 este soluţie şi a ecuaţiei este soluţie şi a ecuaţiei 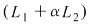
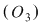 Schimbarea ordinii ecuaţiilor în sistem. Schimbarea ordinii ecuaţiilor în sistem.
Dacă un sistem de ecuaţii se obţine din alt sistem de ecuaţii prin una din transformările de mai sus, atunci cele două sisteme sunt echivalente cum uşor se poate constata.
Prin transformaările enumerate se caută eliminarea succesivă a necunoscutelor.
|