 Optiuni  Inapoi la biblioteca  Da un Test Nou Alege nivelul de dificultate:  Usor Usor Moderat Moderat |
Aranjamente
Autor: Iulia Liberis
Descriere: articol pentru Clasa a X-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Aranjamente: definitie, formula de calcul cu demonstratie, exemple.
Domenii: Elemente de combinatorica

 ARANJAMENTE
ARANJAMENTE
Fie o mulţime 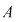 cu cu 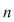 elemente. Dacă elemente. Dacă 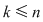 , atunci se pot forma diferite mulţimi ordonate cu câte , atunci se pot forma diferite mulţimi ordonate cu câte 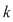 elemente, în care intră numai elemente ale mulţimii elemente, în care intră numai elemente ale mulţimii 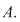
De exemplu, dacă mulţimea 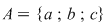 , cu elementele mulţimii , cu elementele mulţimii 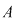 se pot forma următoarele mulţimi ordonate de câte două elemente: se pot forma următoarele mulţimi ordonate de câte două elemente: 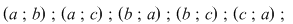
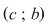 , adică 6 mulţimi ordonate de căte două elemente. , adică 6 mulţimi ordonate de căte două elemente.
Definiţie
Dacă 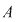 este o mulţime cu este o mulţime cu 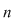 elemente, atunci submulţimile ordonate ale lui elemente, atunci submulţimile ordonate ale lui 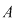 , având fiecare câte , având fiecare câte 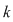 elemente cu elemente cu 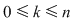 , se numesc aranjamente de , se numesc aranjamente de 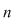 luate câte luate câte 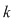 . Se observă că două aranjamente de . Se observă că două aranjamente de 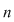 luate câte luate câte 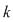 se deosebesc prin 'natura' elementelor lor sau prin ordinea elementelor. se deosebesc prin 'natura' elementelor lor sau prin ordinea elementelor.
Numărul aranjamentelor de 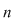 elemente luate câte elemente luate câte 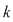 se notează se notează 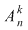 şi se citeşte 'aranjamente de şi se citeşte 'aranjamente de 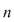 luate câte luate câte 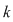 '. '.
Din exemplul anterior 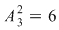
Se observă că 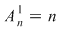 . Într-adevăr, un element din cele . Într-adevăr, un element din cele 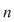 elemente poate fi ales în elemente poate fi ales în 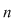 moduri şi cu acest element ales se formează o singură mulţime ordonată. moduri şi cu acest element ales se formează o singură mulţime ordonată.
Teoremă:
Dacă 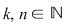 cu cu 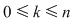 atunci, atunci,
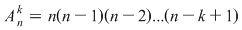
Demonstraţie:
Fie 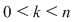 şi se face inducţie după şi se face inducţie după 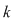 . .
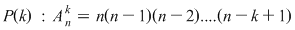
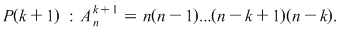
Pentru a repartiza oricare 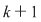 elemente luate din cele elemente luate din cele 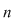 date, pe date, pe 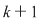 locuri, se pot lua mai întâi locuri, se pot lua mai întâi 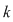 elemente şi aranja pe primele elemente şi aranja pe primele 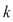 locuri. Acest lucru se poate face în locuri. Acest lucru se poate face în 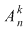 moduri, adică în moduri, adică în 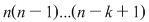 moduri moduri  rămân rămân 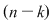 elemente şi oricare din aceste elemente se poate pune pe al elemente şi oricare din aceste elemente se poate pune pe al 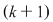 -lea loc. Astfel, în fiecare din cele -lea loc. Astfel, în fiecare din cele 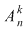 moduri de aranjare a elementelor pe primele moduri de aranjare a elementelor pe primele 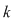 locuri obţinem locuri obţinem 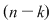 posibilităţi prin care al posibilităţi prin care al 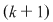 -lea loc este ocupat de unul din cele -lea loc este ocupat de unul din cele 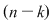 elemente rămase elemente rămase 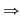 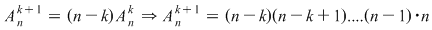
Materiale Didactice Asemanatoare
 Elemente de combinatorica si aplicatii Elemente de combinatorica si aplicatii
 Multimea functiilor injective si bijective Multimea functiilor injective si bijective
|