Multimea functiilor injective si bijective
Autor: Iulia Liberis
Descriere: articol pentru Clasa a X-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Numarul functiilor injective de la o multime cu m elemente la o multime cu n elemente este aranjamente de n luate cate m. Demonstratie. Numarul functiilor bijective de la o multime cu n elemente la o multime cu n elemente este permutari de n. Exemple.
Domenii: Elemente de combinatorica
 MULŢIMEA FUNCŢIILOR INJECTIVE ŞI BIJECTIVE
MULŢIMEA FUNCŢIILOR INJECTIVE ŞI BIJECTIVE
Fie mulţimile 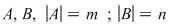 cu cu 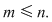 Vrem să determinăm numărul de aplicaţii injective Vrem să determinăm numărul de aplicaţii injective 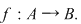
Din definiţia injectivităţii, la argumente diferite 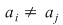 , imaginile sunt diferite, adică , imaginile sunt diferite, adică
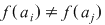 . .
Dacă 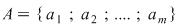 , unei o funcţii injective , unei o funcţii injective 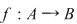 îi corespunde o submulţime ordonată a lui îi corespunde o submulţime ordonată a lui 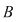 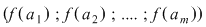 . Numărul submulţimilor ordonate cu . Numărul submulţimilor ordonate cu 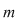 elemente dintr-o mulţime cu elemente dintr-o mulţime cu 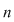 elemente este de elemente este de 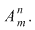
Reciproc, fiecărui aranjament de 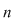 elemente luate câte elemente luate câte 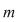 îi corespunde o unică aplicaţie injectivă îi corespunde o unică aplicaţie injectivă 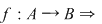 se poate stabili o corespondenţă bijectivă între mulţimea aplicaţiilor injective se poate stabili o corespondenţă bijectivă între mulţimea aplicaţiilor injective 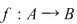 şi mulţimea aranjamentelor de şi mulţimea aranjamentelor de 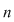 elemente luate câte elemente luate câte 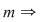 numărul funcţiilor injective numărul funcţiilor injective 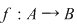 cu cu 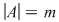 şi şi 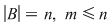 este de este de 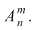
Dacă 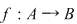 cu cu 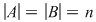 , atunci orice aplicaţie injectivă este bijectivă , atunci orice aplicaţie injectivă este bijectivă 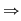 numărul aplicaţiilor bijective de la o mulţime cu numărul aplicaţiilor bijective de la o mulţime cu 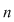 elemente la o alta cu elemente la o alta cu 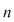 elemente este egal cu elemente este egal cu 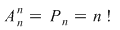
Exemple:
1) Care este numărul funcţiilor injective 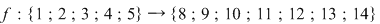
Soluţie:
Fie 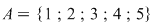 cu cu 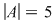
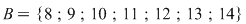 cu cu 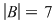 . .
Numărul funcţiilor este de 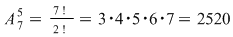 de funcţii. de funcţii.
2) Care este numărul funcţiilor bijective 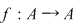 cu cu 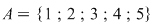 . .
Soluţie: 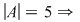 numărul funcţiilor bijective este de numărul funcţiilor bijective este de 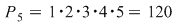 funcţii. funcţii.
Materiale Didactice Asemanatoare
 Aranjamente Aranjamente
 Elemente de combinatorica si aplicatii Elemente de combinatorica si aplicatii
 Permutari. Multimi ordonate cu n elemente Permutari. Multimi ordonate cu n elemente
|