Permutari. Multimi ordonate cu n elemente
Autor: Iulia Liberis
Descriere: articol pentru Clasa a X-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Permutari: definitie, exemplu.
Domenii: Elemente de combinatorica
 PERMUTĂRI. Mulţimi ordonate cu
PERMUTĂRI. Mulţimi ordonate cu 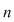 elemente elemente
Fie 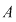 o mulţime finită cu o mulţime finită cu 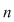 elemente. Această mulţime poate fi ordonată în mai multe moduri, obţinându-se astfel mulţimi ordonate diferite ce se deosebesc între ele doar prin ordinea elementelor. elemente. Această mulţime poate fi ordonată în mai multe moduri, obţinându-se astfel mulţimi ordonate diferite ce se deosebesc între ele doar prin ordinea elementelor.
Definiţie:
Se numeşte permutare a mulţimii 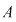 fiecare din mulţimile ordonate ce se formează cu cele fiecare din mulţimile ordonate ce se formează cu cele 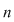 elemente ale mulţimii elemente ale mulţimii 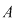 . Se spune că este o permutare a elementelor sale sau o permutare de . Se spune că este o permutare a elementelor sale sau o permutare de 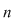 elemente. elemente.
Numărul permutărilor de 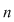 elemente se notează cu elemente se notează cu 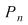 şi se citeşte " permutări de şi se citeşte " permutări de 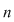 " . Se observă: " . Se observă:
1. O mulţime cu un singur element poate fi ordonată într-un singur mod 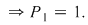
2. O mulţime cu două elemente 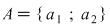 poate fi ordonată: poate fi ordonată: 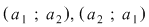
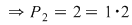
3. O mulţime cu trei elemente 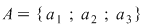 poate fi ordonată: poate fi ordonată: 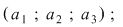
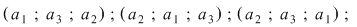
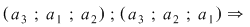
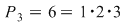 . .
Vrem să determinăm numărul permutărilor unei mulţimi date cu 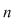 elemente, adică numărul modurilor în care poate fi ordonată o mulţime dată cu elemente, adică numărul modurilor în care poate fi ordonată o mulţime dată cu 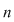 elemente. elemente.
Se convine că mulţimea vidă poate fi ordonată într-un singur mod 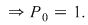 Se defineşte Se defineşte 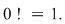 Se va folosi notaţia: Se va folosi notaţia: 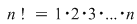 ce reprezintă produsul primelor ce reprezintă produsul primelor 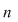 numere naturale nenule. numere naturale nenule.
Teoremă:
Oricare ar fi 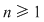 , numărul natural , numărul natural 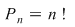 . .
Demonstraţie:
Vom folosi metoda inducţiei matematice:
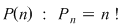
1. 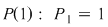 este adevărată fiind demonstrată anterior. este adevărată fiind demonstrată anterior.
2. 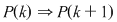
Trebuie să ordonăm în toate modurile posibile o mulţime cu 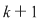 elemente. Oricare din cele elemente. Oricare din cele 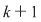 elemente ale mulţimii poate ocupa ultimul loc, adică al elemente ale mulţimii poate ocupa ultimul loc, adică al 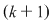 -lea. -lea.
Se obţin astfel 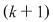 moduri diferite de a ocupa ultimul loc. Să considerăm unul din ele în care un element ales al mulţimii va avea rangul moduri diferite de a ocupa ultimul loc. Să considerăm unul din ele în care un element ales al mulţimii va avea rangul 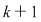 . Rămâne un număr de . Rămâne un număr de 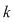 elemente ce trebuie să ocupe primele elemente ce trebuie să ocupe primele 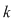 locuri care, din ipoteza de inducţie, acest lucru se poate face în locuri care, din ipoteza de inducţie, acest lucru se poate face în 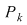 moduri diferite. moduri diferite. 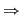 sunt sunt 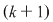 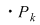 moduri de a ordona o mulţime cu moduri de a ordona o mulţime cu 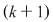 elemente elemente 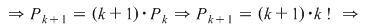
Materiale Didactice Asemanatoare
 Elemente de combinatorica si aplicatii Elemente de combinatorica si aplicatii
 Multimea functiilor injective si bijective Multimea functiilor injective si bijective
|