Combinari
Autor: Iulia Liberis
Descriere: articol pentru Clasa a X-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Combinari: definitie, formula de calcul cu demonstratie, exemple si aplicatii.
Domenii: Elemente de combinatorica
 COMBINĂRI
COMBINĂRI
Fie mulţimea 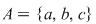 . Vom scrie toate submulţimile mulţimii . Vom scrie toate submulţimile mulţimii 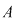 (toate mulţimile ce pot fi formate cu elemente ale mulţimii (toate mulţimile ce pot fi formate cu elemente ale mulţimii 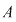 ). ).
Aceste submulţimi sunt:
1) mulţimea vidă : 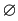
2) submulţimile care au câte un element sunt 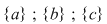
3) submulţimile care au câte două elemente sunt 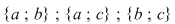
4) submulţimea cu trei elemente (mulţimea totală) este 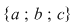 . .
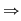 mulţimea mulţimea 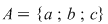 are submulţimi, dintre care: trei submulţimi cu câte un element, trei submulţimi cu câte două elemente, o submulţime cu trei elemente şi mulţimea vidă. are submulţimi, dintre care: trei submulţimi cu câte un element, trei submulţimi cu câte două elemente, o submulţime cu trei elemente şi mulţimea vidă.
Generalizând, fiind dată o mulţime finită cu 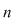 elemente, atunci vrem să determinăm numărul submulţimilor sale cu elemente, atunci vrem să determinăm numărul submulţimilor sale cu 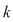 elemente. elemente.
Definiţie
Dacă 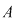 este o mulţime cu este o mulţime cu 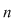 elemente, atunci submulţimile lui elemente, atunci submulţimile lui 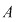 având câte având câte 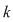 elemente, elemente, 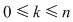 , se numesc combinări de , se numesc combinări de 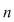 elemente luate câte elemente luate câte 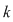 şi se notează şi se notează 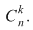
Din exemplul anterior 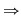 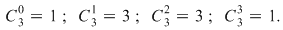
Suma submulţimilor mulţimii 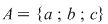 este este
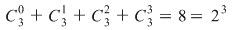 . .
Vrem să determinăm o formulă pentru calculul combinărilor de 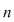 luate câte luate câte 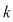 . .
Se observă că 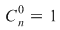 , deoarece fiecare mulţime , deoarece fiecare mulţime 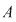 are doar o submulţime fără nici un element, adică mulţimea vidă. are doar o submulţime fără nici un element, adică mulţimea vidă.
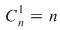 deoarece pentru o mulţime deoarece pentru o mulţime 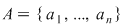 cu cu 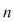 elemente numărul submulţimilor cu un element este elemente numărul submulţimilor cu un element este 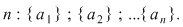
Teoremă:
Dacă 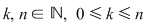 , atunci , atunci
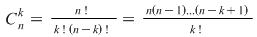
Demonstraţie
Fie 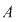 o mulţime cu o mulţime cu 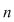 elemente. Fie toate submulţimile lui elemente. Fie toate submulţimile lui 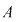 care au care au 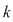 elemente. Dacă ordonăm fiecare dintre aceste submulţimi în toate modurile posibile, obţinem toate submulţimile ordonate ale lui elemente. Dacă ordonăm fiecare dintre aceste submulţimi în toate modurile posibile, obţinem toate submulţimile ordonate ale lui 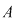 , care au , care au 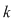 elemente. Numărul acestor submulţimi este: elemente. Numărul acestor submulţimi este: 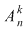 . Dar numărul tuturor submulţimilor lui . Dar numărul tuturor submulţimilor lui 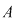 cu cu 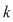 elemente este este egal cu elemente este este egal cu 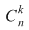 şi fiecare dintre aceste submulţimi poate fi ordonată în şi fiecare dintre aceste submulţimi poate fi ordonată în 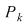 moduri moduri 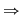
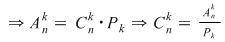
Dar 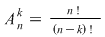 şi şi 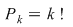
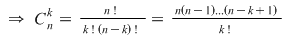
Materiale Didactice Asemanatoare
 Elemente de combinatorica si aplicatii Elemente de combinatorica si aplicatii
|