Combinari
Autor: Iulia Liberis
Descriere: articol pentru Clasa a X-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Combinari: definitie, formula de calcul cu demonstratie, exemple si aplicatii.
Domenii: Elemente de combinatorica
Exemplu:
În câte moduri se poate alcătui din 9 persoane o comisie formată din 5 membri?
Soluţie:
Pentru a avea toate cazurile posibile trebuie să considerăm toate submulţimile formate din câte 5 elemente ale unei submulţimi cu 9 elemente 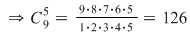
COMBINĂRI COMPLEMENTARE. NUMĂRUL TUTUROR COMBINĂRILOR SUBMULŢIMILOR UNEI MULŢIMI CU 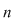 ELEMENTE ELEMENTE
 1. Formula combinărilor complementare:
1. Formula combinărilor complementare:
Dacă 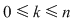 atunci este adevărată egalitatea: atunci este adevărată egalitatea: 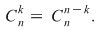
Demonstraţie.
Din formula 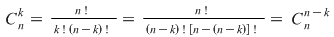
Sensul acestei afirmaţii este următorul:
Dacă 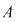 este o mulţime cu este o mulţime cu 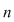 elemente, fiecărei submulţimi elemente, fiecărei submulţimi 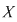 cu cu 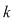 elemente a lui elemente a lui 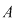 îi asociem o submulţime bine determinată cu îi asociem o submulţime bine determinată cu 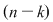 elemente a mulţimii elemente a mulţimii 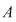 , anume , anume 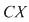 (complementara lui (complementara lui 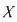 ). ).
Prin această asociere, unei submulţimi cu 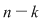 elemente îi corespunde o singură submulţime cu elemente îi corespunde o singură submulţime cu 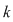 elemente. elemente.
Ceea ce înseamnă că numărul submulţimilor cu 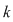 elemente a unei mulţimi elemente a unei mulţimi 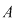 este egal cu numărul submulţimilor cu este egal cu numărul submulţimilor cu 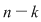 elemente. elemente.
 2. Pentru orice număr natural 2. Pentru orice număr natural 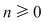 este adevărată egalitatea: este adevărată egalitatea:
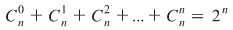 (numărul submulţimilor unei mulţimi cu (numărul submulţimilor unei mulţimi cu 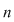 elemente). elemente).
Demonstraţie:
Suma din membrul stâng al egalităţii reprezintă numărul tuturor submulţimilor unei submulţimi cu 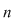 elemente. Egalitatea anterioară se va demonstra prin inducţie: elemente. Egalitatea anterioară se va demonstra prin inducţie:
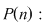 Numărul tuturor submulţimilor unei mulţimi cu Numărul tuturor submulţimilor unei mulţimi cu 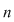 elemente este egal cu elemente este egal cu 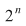 . .
Pentru 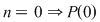 adevărată deoarece submulţimea vidă are o singură submulţime, anume ea însăşi. adevărată deoarece submulţimea vidă are o singură submulţime, anume ea însăşi.
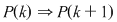
Dacă o mulţime cu 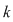 elemente are elemente are 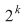 submulţimi vom arăta că o mulţime cu submulţimi vom arăta că o mulţime cu 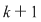 elemente are elemente are 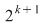 submulţimi. submulţimi.
Fie 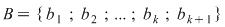 o mulţime cu o mulţime cu 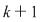 elemente şi elemente şi 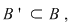
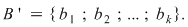
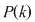 adevărată adevărată 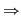 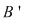 are are 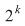 submulţimi. Din fiecare submulţime a lui submulţimi. Din fiecare submulţime a lui 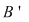 se obţine o nouă submulţime a lui se obţine o nouă submulţime a lui 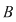 prin adăugarea elementului prin adăugarea elementului 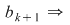 se obţin încă se obţin încă 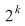 submulţimi ale lui submulţimi ale lui 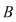 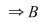 are în total are în total 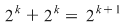 submulţimi. submulţimi.
Materiale Didactice Asemanatoare
 Elemente de combinatorica si aplicatii Elemente de combinatorica si aplicatii
|